题目内容
(本题14分)
已知函数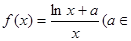 R).
R).
(1)若曲线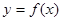 在点
在点 处的切线与直线
处的切线与直线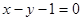 平行,求
平行,求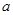 的值;
的值;
(2)在(1)条件下,求函数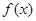 的单调区间和极值;
的单调区间和极值;
(3)当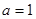 ,且
,且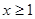 时,证明:
时,证明: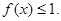
【答案】
解:(I)函数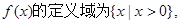
所以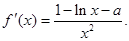
又曲线 处的切线与直线
处的切线与直线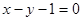 平行,
平行,
所以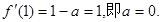
(II)令
当x变化时,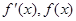 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
+ |
0 |
— |
|
|
|
极大值 |
|
由表可知: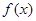 的单调递增区间是
的单调递增区间是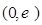 ,单调递减区间是
,单调递减区间是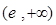
所以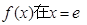 处取得极大值,
处取得极大值,
(III)当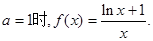
由于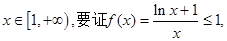
只需证明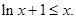
令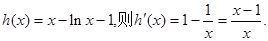
因为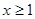 ,所以
,所以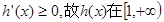 上单调递增,
上单调递增,
当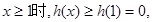 即
即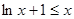 成立。
成立。
故当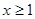 时,有
时,有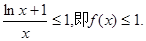
【解析】略

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
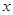


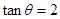
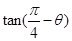 的值;
的值;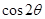 的值.
的值.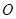 为坐标原点,
为坐标原点,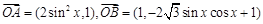 ,
,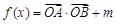 .
.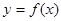 的单调递增区间;
的单调递增区间;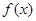 的定义域为
的定义域为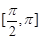 ,值域为
,值域为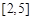 ,求
,求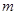 的值.
的值. 是奇函数。(1)求a的值;(2)用定义判断该函数的单调性 (3)若对任意的
是奇函数。(1)求a的值;(2)用定义判断该函数的单调性 (3)若对任意的 ,不等式
,不等式 恒成立,求k的取值范围;
恒成立,求k的取值范围;