题目内容
(理)已知O是平面上的一定点,在△ABC中,动点P满足条件
=
+λ(
+
),(其中λ∈[0,+∞))
,则P的轨迹一定△ABC通过的( )
| OP |
| OA |
| ||
|
|
| ||
|
|
,则P的轨迹一定△ABC通过的( )
分析:由
=
+λ(
+
,知
=λ(
+
),所以
与
+
共线,根据正弦定理知
与
+
共线,由
+
经过线段BC的中点,知点P过三角形重心.
| OP |
| OA |
| ||
|
|
| ||
|
|
| AP |
| ||
|
|
| ||
|
|
| AP |
| ||
|
|
| ||
|
|
| AP |
| AB |
| AC |
| AB |
| AC |
解答:解:∵
=
+λ(
+
),
∴
-
=λ(
+
),
∴
=λ(
+
),
∴
与
+
共线,
根据正弦定理:
=
,
所以|
|sinB=|
|sinC,
所以
与
+
共线,
∵
+
经过线段BC的中点D,
所以P点的轨迹也过中点D,
∴点P过三角形重心.
故选B.
| OP |
| OA |
| ||
|
|
| ||
|
|
∴
| OP |
| OA |
| ||
|
|
| ||
|
|
∴
| AP |
| ||
|
|
| ||
|
|
∴
| AP |
| ||
|
|
| ||
|
|
根据正弦定理:
|
| ||
| sinC |
|
| ||
| sinB |
所以|
| AB |
| AC |
所以
| AP |
| AB |
| AC |
∵
| AB |
| AC |
所以P点的轨迹也过中点D,
∴点P过三角形重心.
故选B.
点评:本题考查三角形五心的性质和应用,是基础题.解题时要认真审题,仔细解答,注意正弦定理的性质和应用.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
 =
= +λ(
+λ(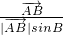 +
+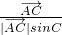 ),(其中λ∈[0,+∞))
),(其中λ∈[0,+∞)) =
= +λ(
+λ( +
+ ),(其中λ∈[0,+∞))
),(其中λ∈[0,+∞))