题目内容
函数y=ln(x-1)+
的定义域为 .
| x2-4 |
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:由对数式的真数大于0,且根式内部的代数式大于等于0联立不等式组求解x的取值集合得答案.
解答:
解:由
,解得x≥2.
∴y=ln(x-1)+
的定义域为{x|x≥2}.
故答案为:{x|x≥2}.
|
∴y=ln(x-1)+
| x2-4 |
故答案为:{x|x≥2}.
点评:本题考查了函数的定义域及其求法,考查了不等式组的解法,是基础题.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
已知a,b∈R,函数f(x)=tanx在x=-
处与直线y=ax+b+
相切,设g(x)=ex+bx2+a,若在区间[1,2]上,不等式m≤g(x)≤m2-2恒成立,则实数m( )
| π |
| 4 |
| π |
| 2 |
| A、有最小值-e |
| B、有最小值e |
| C、有最大值e |
| D、有最大值e+1 |
A={1,2,3,4,5},B={(x,y)|x∈A,y∈A,x-y∈A},则B的非空子集的个数为( )
| A、10 | B、9 |
| C、1024 | D、1023 |
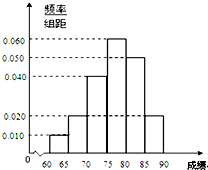 在某次综合素质测试中,共设有40个考室,每个考室30名考生.在考试结束后,统计了他们的成绩,得到如图所示的频率分布直方图.这40个考生成绩的众数
在某次综合素质测试中,共设有40个考室,每个考室30名考生.在考试结束后,统计了他们的成绩,得到如图所示的频率分布直方图.这40个考生成绩的众数