题目内容
在直线l:x+y-5=0上找一点P(x,y),使P对A(1,0),B(3,0)的视角∠APB最大.
考点:解三角形的实际应用
专题:综合题,不等式的解法及应用
分析:设(a,5-a),要使∠APB最大,只要tan∠APB最大,求得tan∠APB=|
|=
,再利用基本不等式求得它的最大值,从而得点P的坐标.
| ||||
1+
|
| 5-a |
| a2-7a+14 |
解答:
解:设P(a,5-a),要使∠APB最大,只要tan∠APB最大.
∵a=5时,∠APB=0,∴a<5,5-a>0.
∵KPA=
,kPB=
,
tan∠APB=|
|=
令t=5-a(t>0),tan∠APB=
=
≤1,当且仅当t=2,即a=3时,取等号.
∴∠APB的最大值为
,此时,点P的坐标为(3,2).
∵a=5时,∠APB=0,∴a<5,5-a>0.
∵KPA=
| 5-a |
| a-1 |
| 5-a |
| a-3 |
tan∠APB=|
| ||||
1+
|
| 5-a |
| a2-7a+14 |
令t=5-a(t>0),tan∠APB=
| t |
| t2-3t+4 |
| 1 | ||
t+
|
∴∠APB的最大值为
| π |
| 4 |
点评:本题主要考查两条直线的夹角公式,以及基本不等式,体现了转化的数学思想,属于中档题.

练习册系列答案
相关题目
设m∈R,则关于x的方程x2+4x+2=m有解的一个必要不充分条件是( )
| A、m>-2 | B、m<-2 |
| C、m>-3 | D、m<-3 |
函数f(x)=3x-x3在区间(a2-10,a)上有最小值,实数a的取值范围是( )
| A、(-1,3) |
| B、(-1,2) |
| C、(-1,3] |
| D、(-1,2] |
 如图,直三棱柱ABC-A1B1C1中,已知∠ACB=90°,AC=BC=1,BB1=2,M,N分别是B1C1和AB的中点.
如图,直三棱柱ABC-A1B1C1中,已知∠ACB=90°,AC=BC=1,BB1=2,M,N分别是B1C1和AB的中点. 如图,三棱锥S-ABC,SA=SB=SC,SG为△SAB上的高,D、E、F为AC、BC、SC的中点.
如图,三棱锥S-ABC,SA=SB=SC,SG为△SAB上的高,D、E、F为AC、BC、SC的中点.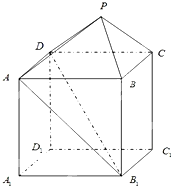 如图所示的几何体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥,其中AB=2,BC=3,AA1=2,点P∈平面CC1D1D且PD=PC=
如图所示的几何体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥,其中AB=2,BC=3,AA1=2,点P∈平面CC1D1D且PD=PC=