题目内容
已知tanx=-
，则tan2x=（ ）
| 3 |
| 4 |
A、
| ||
B、-
| ||
C、-
| ||
D、
|
考点：二倍角的正切
专题：三角函数的求值
分析：利用二倍角的正切公式即可求得答案．
解答：
解：∵tanx=-
，
∴tan2x=
=
=-
，
故选：C．
| 3 |
| 4 |
∴tan2x=
| 2tanx |
| 1-tan2x |
2×(-
| ||
1-(-
|
| 24 |
| 7 |
故选：C．
点评：本题考查二倍角的正切，熟练掌握公式是解决问题的关键，属于基础题．
练习册系列答案
相关题目
从学号为0～50的燕中高二某班50名学生中随机选取5名同学参加数学测试，采用系统抽样的方法，则所选5名学生的学号可能是（ ）
| A、1，2，3，4，5 |
| B、5，16，27，38，49 |
| C、2，4，6，8，10 |
| D、4，13，22，31，40 |
将抛物线y=3x2如何平移，可得到抛物线y=3（x-2）2-1（ ）
| A、向左平移2个单位，再向上平移1个单位 |
| B、向左平移2个单位，再向下平移1个单位 |
| C、向右平移2个单位，再向上平移1个单位 |
| D、向右平移2个单位，再向下平移1个单位 |
在△ABC中，∠A、∠B、∠C所对的边分别是2、3、4，则三角形中最大角的余弦值为（ ）
A、
| ||
B、
| ||
C、
| ||
D、-
|
已知实数x，y满足
，若y≥k（x+2）恒成立，则实数k的取值范围为（ ）
|
A、[0，
| ||
B、（-∞，0]∪[
| ||
C、[-1，
| ||
D、（-∞，-1]∪[
|
函数y=
的图象如图所示，则（ ）
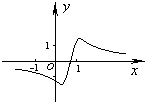
| 2(x+a) |
| (x+a)2+b |
| A、a∈（0，1），b∈（0，1） |
| B、a∈（0，1），b∈（1，+∞） |
| C、a∈（-1，0），b∈（1，+∞） |
| D、a∈（-1，0），b∈（0，1） |
给定下列四个命题：
①若一个平面内的两条直线与另一个平面都平行，则这两个平面平行；
②若两个平面都垂直于同一条直线，则这两个平面平行；
③若两个平面互相垂直，则在其中一个平面内的直线垂直另外一个平面；
④两个平行直线能确定一个平面，其中正确的命题是（ ）
①若一个平面内的两条直线与另一个平面都平行，则这两个平面平行；
②若两个平面都垂直于同一条直线，则这两个平面平行；
③若两个平面互相垂直，则在其中一个平面内的直线垂直另外一个平面；
④两个平行直线能确定一个平面，其中正确的命题是（ ）
| A、①和② | B、②和③ |
| C、③和④ | D、②和④ |
如图，已知向量| p |
| q |
| π |
| 4 |
| p |
| 2 |
| q |
| AB |
| p |
| q |
| AC |
| p |
| q |
| AD |
A、
| ||||
B、
| ||||
| C、7 | ||||
| D、18 |