题目内容
设α是空间中的一个平面,l,m,n是三条不同的直线,则下列命题中正确的是( )
| A、若l∥m,m⊥α,n⊥α,则l∥n |
| B、若m?α,n?α,则l∥m |
| C、若m?α,n?α,l⊥m,则l⊥α |
| D、若l⊥m,l⊥n,则n∥m |
考点:空间中直线与平面之间的位置关系
专题:空间位置关系与距离
分析:利用直线垂直于平面的性质和平行公理能判断A的正误;利用两直线的位置关系能判断B和D的正误;利用直线垂直于平面的判定定理能判断C的正误.
解答:
解:若l∥m,m⊥α,n⊥α,
则由直线垂直于平面的性质知m∥n,
再由平行公理得以l∥n,故A正确;
若m?α,n?α,l⊥n,
则l与m可能平行、相交、也可能异面,故B错误;
m?α,n?α,l⊥m,l⊥n,
需要m∩n=A才有l⊥α,故C错误;
若l⊥m,l⊥n,
则n与m可能平行、相交、也可能异面,故D错误.
故选:A.
则由直线垂直于平面的性质知m∥n,
再由平行公理得以l∥n,故A正确;
若m?α,n?α,l⊥n,
则l与m可能平行、相交、也可能异面,故B错误;
m?α,n?α,l⊥m,l⊥n,
需要m∩n=A才有l⊥α,故C错误;
若l⊥m,l⊥n,
则n与m可能平行、相交、也可能异面,故D错误.
故选:A.
点评:本题考查空间直线与直线、直线与平面的位置关系的判断,是基础题,解题时要注意空间思维能力的培养.

练习册系列答案
相关题目
已知{an}为等差数列,且a2+a8=8,a6=5,则Sl0的值为( )
| A、50 | B、45 | C、55 | D、40 |
已知集合M={x∈R||x|>2},N={x∈R|x2-4x+3<0},则集合(∁RM)∩N 等于( )
| A、{x|x<2} |
| B、{x|-2≤x≤2} |
| C、{x|-2≤x<1} |
| D、{x|1<x≤2} |
将函数f(x)=3sin(
+
)的图象向右平移
个单位长度,再把图象上所有点的横坐标 伸长到原来的2倍(纵坐标不变),得到y=g(x)的图象,则y=g(x)的解析式为( )
| x |
| 2 |
| π |
| 3 |
| π |
| 3 |
A、g(x)=3sin(x+
| ||||
B、g(x)=3sin(x+
| ||||
C、g(x)=3sin(
| ||||
D、g(x)=3sin(
|
已知函数f(x)=2|x|,那么函数f(x)( )
| A、是奇函数,且在(-∞,0)上是增函数 |
| B、是偶函数,且在(-∞,0)上是减函数 |
| C、是奇函数,且在(0,+∞)上是增函数 |
| D、是偶函数,且在(0,+∞)上是减函数 |
已知M(sinα,cosα),N(cosα,sinα),直线l:xcosα+ysinα+p=0 (p<-1),若M,N到l的距离分别为m,n,则( )
| A、m≥n | B、m≤n |
| C、m≠n | D、以上都不对 |
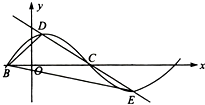 已知函数f(x)=sin(2πx+φ)的部分图象如图所示,点B,C是该图象与x轴的交点,过点C的直线与该图象交于D,E两点,则(
已知函数f(x)=sin(2πx+φ)的部分图象如图所示,点B,C是该图象与x轴的交点,过点C的直线与该图象交于D,E两点,则(