题目内容

已知△ABC中，cosB=
b2+a2-c22ac
，则△ABC为
 
三角形．
分析：根据余弦定理表示出cosB，与已知的cosB相等，化简后即可得到b=c，进而得到三角形为等腰三角形．
解答：解：根据余弦定理得cosB=
a2+c2-b2
2ac
，
又cosB=
b2+a2-c2
2ac
，
∴
a2+c2-b2
2ac
=
b2+a2-c2
2ac
，即a2+c2-b2=b2+a2-c2，
化简得：b2=c2，由b和c都大于0，解得b=c，
则△ABC为等腰三角形．
故答案为：等腰三角形
点评：此题考查了余弦定理，等腰三角形的定义，以及三角形形状的判断，熟练掌握余弦定理是解本题的关键．
练习册系列答案
相关题目
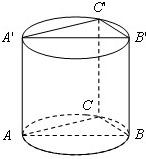精英家教网如图，直三棱柱ABC-A′B′C′内接于高为
2
的圆柱中，已知∠ACB=90°，AA′=
2
，BC=AC=1，O为AB的中点．
求（1）圆柱的全面积；
（2）异面直线AB′与CO所成的角的大小；
（3）求二面角A′-BC-A的大小．
精英家教网已知O是△ABC内任意一点，连接AO，BO，CO并延长交对边于A′，B′，C′，则
OA/
AA/
+
OB/
BB/
+
OC/
CC/
=1，这是平面几何中的一个命题，其证明方法常采用“面积法”：
OA/
AA/
+
OB/
BB/
+
OC/
CC/
=
S△OBC
S△ABC
+
S△OCA
S△ABC
+
S△OAB
S△ABC
=
S△ABC
S△ABC
=1．运用类比猜想，对于空间四面体存在什么类似的命题？并用“体积法”证明．
已知O是△ABC内任意一点，连结AO，BO，CO并延长交对边于A′，B′，C′，则
OA′
AA′
+
OB′
BB′
+
OC′
CC′
=1，这是平面几何中的一个命题，运用类比猜想，对于空间四面体ABCD中，若O四面体ABCD内任意点存在什么类似的命题
VO-BCD
VABCD
+
V0-ABD
VABCD
+
VO-ACD
VABCD
+
VO-ABC
VABCD
=1
VO-BCD
VABCD
+
V0-ABD
VABCD
+
VO-ACD
VABCD
+
VO-ABC
VABCD
=1
．
在△ABC中，角A，B，C的对边分别为a，b，c，已知向量
m
=（2a-c，b）与向量
n
=（cosB，-cosC）互相垂直．
（1）求角B的大小；
（2）求函数y=2sin2C+cos（B-2C）的值域；
（3）若AB边上的中线CO=2，动点P满足
AP
=sin2θ•
AO
+cos2θ•
AC
(θ∈R)，求(
PA
+
PB
)•
PC
的最小值．
已知O是△ABC内任意一点，连接AO、BO、CO并延长交对边于A′、B′、C′，则
OA′
AA′
+
OB′
BB′
+
OC′
CC′
=1，运用类比猜想，对于空间中四面体A-BCD有
OA′
AA′
+
OB′
BB′
+
OC′
CC′
+
OD′
DD′
=1
OA′
AA′
+
OB′
BB′
+
OC′
CC′
+
OD′
DD′
=1
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网