题目内容
已知O是△ABC内任意一点，连结AO，BO，CO并延长交对边于A′，B′，C′，则| OA′ |
| AA′ |
| OB′ |
| BB′ |
| OC′ |
| CC′ |
| VO-BCD |
| VABCD |
| V0-ABD |
| VABCD |
| VO-ACD |
| VABCD |
| VO-ABC |
| VABCD |
| VO-BCD |
| VABCD |
| V0-ABD |
| VABCD |
| VO-ACD |
| VABCD |
| VO-ABC |
| VABCD |
分析：由条件利用平面图形的线段的性质类比立体图形中的体积的性质，可得结论．
解答：解：O是△ABC内任意一点，连结AO，BO，CO并延长交对边于A′，B′，C′，则
+
+
=1，
利用类比推理，猜想，对于空间四面体ABCD中，若O四面体ABCD内任意点O，
应有
+
+
+
=1，
故答案为
+
+
+
=1．
| OA′ |
| AA′ |
| OB′ |
| BB′ |
| OC′ |
| CC′ |
利用类比推理，猜想，对于空间四面体ABCD中，若O四面体ABCD内任意点O，
应有
| VO-BCD |
| VABCD |
| V0-ABD |
| VABCD |
| VO-ACD |
| VABCD |
| VO-ABC |
| VABCD |
故答案为
| VO-BCD |
| VABCD |
| V0-ABD |
| VABCD |
| VO-ACD |
| VABCD |
| VO-ABC |
| VABCD |
点评：本题主要考查类比推理，用平面中图形的线段的性质类比立体图形中的体积的性质，属于基础题．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
=
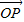[（1-λ）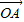
+（1-λ）
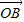+（1+2λ）
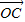]（λ∈R且λ≠0），则点P的轨迹一定通过△ABC的 ．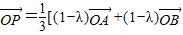
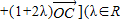且λ≠1，则P的轨迹一定通过△ABC的（ ）