题目内容
已知O是△ABC内任意一点，连接AO、BO、CO并延长交对边于A′、B′、C′，则
+
+
=1，运用类比猜想，对于空间中四面体A-BCD有
+
+
+
=1
+
+
+
=1．
| OA′ |
| AA′ |
| OB′ |
| BB′ |
| OC′ |
| CC′ |
| OA′ |
| AA′ |
| OB′ |
| BB′ |
| OC′ |
| CC′ |
| OD′ |
| DD′ |
| OA′ |
| AA′ |
| OB′ |
| BB′ |
| OC′ |
| CC′ |
| OD′ |
| DD′ |
分析：先根据所给的定理写出猜想的定理，把面积类比成体积，把面积之和等于1，写成体积之和等于1，再进行证明．
解答：解：猜想：若O四面体ABCD内任意点，AO，BO，CO，DO并延长交对面于A′，B′，C′，D′，则
+
+
+
=1
用“体积法”证明如下：
+
+
+
=
+
+
+
=
=1
故答案为：
+
+
+
=1
| OA′ |
| AA′ |
| OB′ |
| BB′ |
| OC′ |
| CC′ |
| OD′ |
| DD′ |
用“体积法”证明如下：
| OA′ |
| AA′ |
| OB′ |
| BB′ |
| OC′ |
| CC′ |
| OD′ |
| DD′ |
=
| VO-BCD |
| VA-BCD |
| VO-CAD |
| VA-BCD |
| VO-ABD |
| VC-ABD |
| VO-ABC |
| VD-ABC |
| VABCD |
| VABCD |
故答案为：
| OA′ |
| AA′ |
| OB′ |
| BB′ |
| OC′ |
| CC′ |
| OD′ |
| DD′ |
点评：本题考查类比推理，是一个基础题，这种题目的解题的关键是要根据所给的定理类比出可能的定理，后面再进行证明．
练习册系列答案
教材全解字词句篇系列答案
相关题目
=
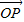[（1-λ）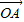
+（1-λ）
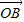+（1+2λ）
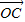]（λ∈R且λ≠0），则点P的轨迹一定通过△ABC的 ．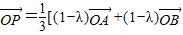
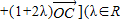且λ≠1，则P的轨迹一定通过△ABC的（ ）