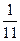题目内容
在三角形ABC中任取一点P，求三角形ABP与三角形ABC的面积之比大于
的概率．
| n-1 |
| n |
根据题意画出图象如图所示：
当三角形ABP与三角形ABC的面积之比等于
时，点P在EF上活动，
则有
=
，
所以此时
=
．
若三角形ABP与三角形ABC的面积之比大于
，则点P在阴影部分活动，
所以三角形ABP与三角形ABC的面积之比大于
的概率为
=(
)2=
，
所以三角形ABP与三角形ABC的面积之比大于
的概率
．
当三角形ABP与三角形ABC的面积之比等于
| n-1 |
| n |
则有
| PH |
| CG |
| n-1 |
| n |
所以此时
| EF |
| AB |
| 1 |
| n |
若三角形ABP与三角形ABC的面积之比大于
| n-1 |
| n |
所以三角形ABP与三角形ABC的面积之比大于
| n-1 |
| n |
| S△CEF |
| S△CAB |
| EF |
| AB |
| 1 |
| n2 |
所以三角形ABP与三角形ABC的面积之比大于
| n-1 |
| n |
| 1 |
| n |
练习册系列答案
阅读快车系列答案
相关题目
