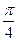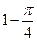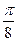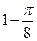题目内容
已知关于x的一次函数y=mx+n.
(1)设集合P={-2,-1,1,2,3}和Q={-2,3},分别从集合P和Q中随机取一个数作为m和n,求函数y=mx+n是增函数的概率;
(2)实数m,n满足条件
求函数y=mx+n的图象经过一、二、三象限的概率.
(1)设集合P={-2,-1,1,2,3}和Q={-2,3},分别从集合P和Q中随机取一个数作为m和n,求函数y=mx+n是增函数的概率;
(2)实数m,n满足条件
|
(1)抽取的全部结果所构成的基本事件空间为:
Ω={(-2,-2),(-2,3),(-1,-2),(-1,3),
(1,-2),(1,3),(2,-2),(2,3),(3,-2),
(3,3)}共10个基本事件(2分)
设使函数为增函数的事件空间为A:
则A={(1,-2),(1,3),(2,-2),(2,3),(3,-2),
(3,3)}有6个基本事件(4分)
所以,P(A)=
=
(6分)
(2)m、n满足条件m+n-1≤0,-1≤m≤1,-1≤n≤1的区域如图所示:
使函数图象过一、二、三象限的(m,n)为区域为第一象限的阴影部分
∴所求事件的概率为P=
=
.(12分)

Ω={(-2,-2),(-2,3),(-1,-2),(-1,3),
(1,-2),(1,3),(2,-2),(2,3),(3,-2),
(3,3)}共10个基本事件(2分)
设使函数为增函数的事件空间为A:
则A={(1,-2),(1,3),(2,-2),(2,3),(3,-2),
(3,3)}有6个基本事件(4分)
所以,P(A)=
| 6 |
| 10 |
| 3 |
| 5 |
(2)m、n满足条件m+n-1≤0,-1≤m≤1,-1≤n≤1的区域如图所示:
使函数图象过一、二、三象限的(m,n)为区域为第一象限的阴影部分
∴所求事件的概率为P=
| ||
|
| 1 |
| 7 |


练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目