题目内容
7.某市春节期间7家超市的广告费支出xi(万元)和销售额yi(万元)数据如下:| 超市 | A | B | C | D | E | F | G |
| 广告费支出xi | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
| 销售额yi | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
(2)用对数回归模型拟合y与x的关系,可得回归方程:$\widehaty=12lnx+22$,
经计算得出线性回归模型和对数模型的R2分别约为0.75和0.97,请用R2说明选择哪个回归模型更合适,并用此模型预测A超市广告费支出为8万元时的销售额.
参数数据及公式:$\overline x=8\;\;,\;\;\overline y=42$,$\sum_{i=1}^7{{x_i}{y_i}}=2794\;\;,\;\;\sum_{i=1}^7{{x_i}^2}=708$,$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n•\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}\;\;,\;\;\widehata=\overline y-\widehatb\overline x$,ln2≈0.7.
分析 (1)求出回归系数,可得y关于x的线性回归方程;
(2)对数回归模型更合适.当x=8万元时,预测A超市销售额为47.2万元.
解答 解:(1)$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n•\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}=\frac{2794-7×8×42}{{708-7×{8^2}}}=1.7$,$\widehata=\overline y-\widehatb\overline x=28.4$
所以,y关于x的线性回归方程是$\widehaty=1.7x+28.4$
(2)∵0.75<0.97,∴对数回归模型更合适.
当x=8万元时,预测A超市销售额为47.2万元.
点评 本题考查线性回归方程,考查学生的计算能力,比较基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.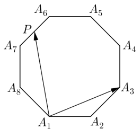 如图所示,正八边形A1A2A3A4A5A6A7A8的边长为2,若P为该正八边形边上的动点,则$\overrightarrow{{A_1}{A_3}}•\overrightarrow{{A_1}P}$的取值范围为( )
如图所示,正八边形A1A2A3A4A5A6A7A8的边长为2,若P为该正八边形边上的动点,则$\overrightarrow{{A_1}{A_3}}•\overrightarrow{{A_1}P}$的取值范围为( )
 如图所示,正八边形A1A2A3A4A5A6A7A8的边长为2,若P为该正八边形边上的动点,则$\overrightarrow{{A_1}{A_3}}•\overrightarrow{{A_1}P}$的取值范围为( )
如图所示,正八边形A1A2A3A4A5A6A7A8的边长为2,若P为该正八边形边上的动点,则$\overrightarrow{{A_1}{A_3}}•\overrightarrow{{A_1}P}$的取值范围为( )| A. | $[0,8+6\sqrt{2}]$ | B. | $[-2\sqrt{2},8+6\sqrt{2}]$ | C. | $[-8-6\sqrt{2},2\sqrt{2}]$ | D. | $[-8-6\sqrt{2},8+6\sqrt{2}]$ |
18.在△ABC中,角A,B,C所对的边分别是a,b,c,若a2+b2=2c2,则角C的取值范围是( )
| A. | $({0,\frac{π}{3}}]$ | B. | $({0,\frac{π}{3}})$ | C. | $({0,\frac{π}{6}}]$ | D. | $({0,\frac{π}{6}})$ |
2.二项式(x-a)7的展开式中,含x4项的系数为-280,则${∫}_{a}^{2e}$$\frac{1}{x}$dx=( )
| A. | ln2 | B. | ln2+1 | C. | 1 | D. | $\frac{{{e^2}-1}}{{4{e^2}}}$ |
12.在△ABC中,角A,B,C对应边分别为a,b,c,已知三个向量$\overrightarrow m=(a,cos\frac{A}{2})$,$\overrightarrow n=(b,cos\frac{B}{2})$,$\overrightarrow p=(c,cos\frac{C}{2})$共线,则△ABC形状为( )
| A. | 等边三角形 | B. | 等腰三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
16.已知集合A={x|x2-9>0},B={x|2<x≤5},则A∩B=( )
| A. | (3,5] | B. | (-∞,-3)∪(5,+∞) | C. | (-∞,-3)∪[5,+∞) | D. | (-∞,2]∪(3,+∞) |
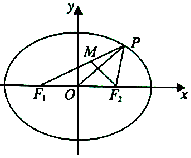 如图所示,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$,其中a>b>0,F1,F2分别为其左,右焦点,点P是椭圆C上一点,PO⊥F2M,且$\overrightarrow{{F_1}M}=λ\overrightarrow{MP}$.
如图所示,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$,其中a>b>0,F1,F2分别为其左,右焦点,点P是椭圆C上一点,PO⊥F2M,且$\overrightarrow{{F_1}M}=λ\overrightarrow{MP}$.



