题目内容
已知lgx+lgy=2lg(x-2y),则log2
等于( )
| x |
| y |
| A、1或2 | B、0或2 | C、2 | D、4 |
考点:对数的运算性质
专题:函数的性质及应用
分析:由已知得(
)2-5(
)+4=0,解得
=1,(舍),或
=4,由此能求出log2
=2.
| x |
| y |
| x |
| y |
| x |
| y |
| x |
| y |
| x |
| y |
解答:
解:∵lgx+lgy=2lg(x-2y),
∴lg(xy)=lg(x-2y)2,
∴xy=x2-4xy+4y2,
∴x2+4y2-5xy=0,
∴(
)2-5(
)+4=0,
解得
=1,(舍),或
=4,
∴log2
=2.
故选:C.
∴lg(xy)=lg(x-2y)2,
∴xy=x2-4xy+4y2,
∴x2+4y2-5xy=0,
∴(
| x |
| y |
| x |
| y |
解得
| x |
| y |
| x |
| y |
∴log2
| x |
| y |
故选:C.
点评:本题考查对数式的值的求法,解题时要认真审题,注意对数性质的合理运用.

练习册系列答案
相关题目
设方程2lnx=7-2x的解为x0,则关于x的不等式(x+1)(x-3-x0)<0的最大整数解为( )
| A、4 | B、5 | C、6 | D、7 |
集合M={-2,0,1,2},N={x||2x-1|>1},则M∩N=( )
| A、{-2,1,2} |
| B、{0,2} |
| C、{-2,2} |
| D、[-2,2] |
表示如图中阴影部分所示平面区域的不等式组是( )
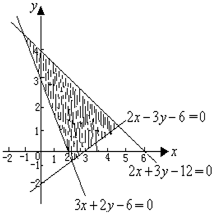

A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|