题目内容

精英家教网如图所示，△ABC中，BC边上的两点D，E分别与A连线．假设∠ACB=∠ADC=
π4
，三角形ABC，ABD，ABE的外接圆直径分别为d，e，f，则d，e，f满足的不等关系是
 
．
分析：先由题意可知AD=AC，AE＜AC，再根据正弦定理分别用AD，AC，AE，sinB表示出d，e，f，进而得到答案．
解答：解：由题意可知，AD=AC，AE＜AC，
根据正弦定理可知：d=
AC
sinB
，e=
AD
sinB
，f=
AE
sinB
，
∴d=e＜f，
故选D=e＜f．
点评：本题主要考查了正弦定理在实际中的应用．属基础题．
练习册系列答案
相关题目
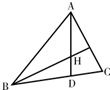精英家教网如图所示在△ABC中，sin2A+sin2C=sin2B+sinA．sinC
（1）求B的度数．
（2）设H为△ABC的垂心，且
BH
•
BC
=6求AC边长的最小值．
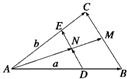精英家教网如图所示，△ABC中，AB=AC=2
3
，∠B1AB=∠B1BA=30°，过B1作B1A1∥BA，过A1作A1B2∥AB1，过B2作B2A2∥B1A1，过A2作A2B3∥A1B2，过B3作B3A3∥B2A2，…．若将线段BnAn的长度记为an，线段AnBn+1的长度记为bn，（n=1，2，3…），则a1+b1=
 
，
lim
n→∞
[(a1+b1)+(a2+b2)+…+(an+bn)]=
 
．
精英家教网如图所示，△ABC中，
AD
=
2
3
AB
，DE∥BC交AC于E，AM是BC边上中线，交DE于N．设
AB
=a，
AC
=b，用a，b分别表示向量
AE
，
BC
，
DE
，
DN
，
AM
，
AN
．
如图所示，△ABC中，已知顶点A（3，-1），∠B的内角平分线方程是x-4y+10=0过点C的中线方程为6x+10y-59=0．求顶点B的坐标和直线BC的方程．
如图所示，△ABC中，EF是BC边的垂直平分线，且
AE
=λ
AB
，
AB
=a，
AC
=b，则λ=（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网