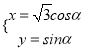题目内容
【题目】设![]() ,点
,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,且
轴上,且![]() ,
,![]() .
.
(1)当点![]() 在
在![]() 轴上运动时,求点
轴上运动时,求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设点![]() 是轨迹
是轨迹![]() 上的动点,点
上的动点,点![]() 在
在![]() 轴上,圆
轴上,圆![]() 内切于
内切于![]()
![]() ,求
,求![]()
![]() 的面积的最小值.
的面积的最小值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)依据题设条件直接建立坐标之间的等量关系(轨迹方程);(2)依据题设条件建立关于三角形面积公式的函数关系,最后再运用所学知识求其最小值:
试题解析:
解:(1)设![]() ,由
,由![]() ,得点
,得点![]() 为线段
为线段![]() 的中点,
的中点,
∴![]() ,
,![]() ,∴
,∴![]() ,
,![]() .
.
由![]() ,得
,得![]() .
.
所以动点![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() .
.
(2)设![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,
∴直线![]() 的方程为
的方程为![]() ,整理得:
,整理得:![]()
![]() .
.
∵圆![]() 内切于
内切于![]() ,可得
,可得![]() 与圆相切,∴
与圆相切,∴![]() ,
,
注意到![]() ,化简得:
,化简得:![]() ,
,
同理可得:![]() ,
,
因此,![]() 是方程
是方程![]() 的两个不相等的实数根.
的两个不相等的实数根.
根据根与系数的关系,化简整理可得![]()
![]()
![]() ,
,
由此可得![]() 的面积为
的面积为![]()
![]() ,
,
∴当![]() 时,即当
时,即当![]() 时,
时,![]() 的面积的最小值为8.
的面积的最小值为8.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目