Question

【题目】在直角坐标系xOy中，直线l的方程为x﹣y+4=0，曲线C的参数方程为．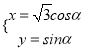

（1）已知在极坐标系（与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，点P的极坐标为，判断点P与直线l的位置关系；

（2）设点Q是曲线C上的一个动点，求它到直线l的距离的最小值．

Answer 1

【答案】（1）点P在直线l上；（2）.

【解析】试题分析：（1）消去曲线参数方程中的参数，得到曲线普通方程，根据公式，把点的坐标化为直角坐标方程，即可判断点与直线的关系；（2）设，由点到直线的距离公式可得距离的表达式，通过三角恒等变换化为正弦型函数在给定区间上的最值来求解.

试题解析：（1）∵曲线C的参数方程为，

∴曲线C的普通方程是，

∵点P的极坐标为，

∴点P的普通坐标为（4cos，4sin），即（0，4），

把（0，4）代入直线l：x﹣y+4=0，

得0﹣4+4=0，成立，

故点P在直线l上．

（2）∵Q在曲线C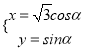： 上，（0°≤α＜360°）

∴到直线l：x﹣y+4=0的距离：

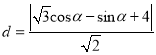
=，（0°≤α＜360°）

∴．