题目内容
高射炮击中目标的概率与射击角度成正比,射击角度为(Ⅰ)现甲、乙、丙依次射击,若击中则停止射击,若击不中则下一门射击,但丙击中与否都要停止射击,求目标被击中的概率;
(Ⅱ)三门炮同时向目标射击,求击中目标的炮的门数ξ的数学期望.
解:(Ⅰ)设甲、乙、丙击中目标分别为事件A、B、C,射击角度为α,P=kx,由P=0.6=k·![]() ,得k=
,得k=![]() ,
,
∴P(A)=![]() ×
×![]() =
=![]() ,P(B)=
,P(B)=![]() ,P(C)=
,P(C)=![]() ,
,
∴所求事件概率为P(A)+P(![]() ·B)+P(
·B)+P(![]() ·
·![]() ·C)=
·C)=![]() ;
;
(Ⅱ)ξ的取值为0,1,2,3,则P(ξ=0)=![]() ,
,
P(ξ=1)=![]() ,
,
P(ξ=2)=![]() ,
,
P(ξ=3)=![]() ,
,
∴Eξ=0×![]() +l×
+l×![]() +2×
+2×![]() +3×
+3×![]() =
=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
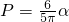 ,现有甲、乙、丙三门高射炮,每门高射炮击中目标与否相互独立,已知甲、乙、丙射击的角度分别为
,现有甲、乙、丙三门高射炮,每门高射炮击中目标与否相互独立,已知甲、乙、丙射击的角度分别为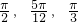 .
.