题目内容
已知动圆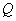 过定点
过定点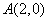 且与
且与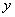 轴截得的弦
轴截得的弦 的长为
的长为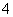 .
.
(Ⅰ)求动圆圆心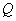 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)已知点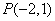 ,动直线
,动直线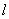 和坐标轴不垂直,且与轨迹
和坐标轴不垂直,且与轨迹 相交于
相交于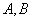 两点,试问:在
两点,试问:在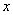 轴上是否存在一定点
轴上是否存在一定点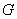 ,使直线
,使直线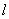 过点
过点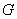 ,且使得直线
,且使得直线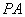 ,
,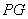 ,
,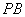 的斜率依次成等差数列?若存在,请求出定点
的斜率依次成等差数列?若存在,请求出定点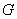 的坐标;否则,请说明理由.
的坐标;否则,请说明理由.
解:(Ⅰ)设 ,根据题意得
,根据题意得 , …………2分
, …………2分
整理得 ,所以动圆圆心
,所以动圆圆心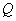 的轨迹
的轨迹 的方程是
的方程是 . ………4分
. ………4分
(Ⅱ)设存在符合题意的定点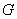 .
.
设直线的方程为 且
且 ,则
,则 . …………5分
. …………5分
将 代入
代入 ,整理得
,整理得 .
.
由题意得 ,即
,即 .
.
设 ,
, ,则
,则 ,
, ,
,
 ,
, ,
,
 ,
,
由题意得 ,即
,即 ,
,
所以 , ……………………7分
, ……………………7分
即
……………9分
把 ,
, 代入上式,
代入上式,
整理得 , ………11分
, ………11分
又因为 ,所以
,所以 ,解得
,解得
所以存在符合题意的定点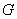 ,且点
,且点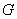 的坐标为
的坐标为 . …………………13分
. …………………13分

练习册系列答案
相关题目
 等于 ( )
等于 ( )  B.
B.  C.
C.  D.
D.
 与
与 轴围成的封
轴围成的封 闭区域的面积为 .
闭区域的面积为 . 的各项均为正数,且
的各项均为正数,且 ,则
,则 =
=
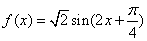 ,有下列四个结论:
,有下列四个结论: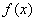 在区间
在区间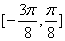 上是增函数:
上是增函数: 是函数
是函数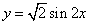 的图象向左平移
的图象向左平移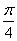 得到;
得到;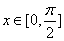 ,则函数
,则函数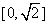 .
.  ,则“
,则“ ”是“
”是“ 为纯虚数”的
为纯虚数”的 与销售额
与销售额 的统计数据如下表,根据下表可得回归方程
的统计数据如下表,根据下表可得回归方程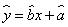 中的
中的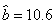 ,据此模型预报广告费用为10万元时销售额为
,据此模型预报广告费用为10万元时销售额为
 ,
, ,则数列
,则数列 的通项为
的通项为 ( )
( ) B.
B. C.
C. D.
D.