题目内容
(本小题满分10分)选修4-5:不等式选讲
设函数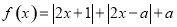 ,
,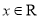 .
.
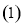 当
当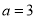 时,求不等式
时,求不等式 的解集;
的解集;
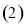 对任意
对任意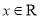 恒有
恒有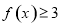 ,求实数
,求实数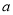 的取值范围.
的取值范围.
(1)  ;(2)
;(2) 
【解析】
试题分析:(1)根据题意得当 时,代入并去掉绝对值得到一具分段函数:
时,代入并去掉绝对值得到一具分段函数: ,所以可得:
,所以可得: 的解集为
的解集为 ;(2)根据含有绝对值的不等式的大小规律可去掉绝对值可得:
;(2)根据含有绝对值的不等式的大小规律可去掉绝对值可得: ,最后由
,最后由 恒成立,得:
恒成立,得: ,解得
,解得 ,所以
,所以 的取值范围是
的取值范围是 .
.
试题解析:(1)当 时,
时,
所以 的解集为
的解集为 (5分)
(5分)
(2)
由 恒成立,有
恒成立,有 ,解得
,解得
所以 的取值范围是
的取值范围是 (10分)
(10分)
考点:1.绝对值不等式;2.不等式的证明

练习册系列答案
相关题目
 的大小关系是 ( )
的大小关系是 ( ) B.
B. C.
C. D.
D.
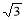 ,CC1=
,CC1=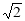 ,则二面角C1—BD—C的大小为( )
,则二面角C1—BD—C的大小为( )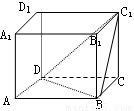
 ,则
,则 = _________.
= _________. ,
, ,
, ,则( )
,则( ) B.
B. C.
C. D.
D.
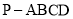 中,
中,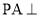 平面
平面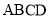 ,
,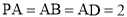 ,四边形
,四边形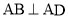 ,
,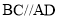 且
且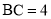 ,点
,点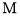 为
为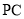 中点.
中点.
 求证:平面
求证:平面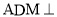 平面
平面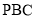 ;
;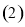 求点
求点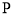 到平面
到平面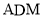 的距离.
的距离.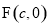 是双曲线
是双曲线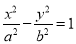 (
(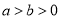 )的右焦点,过
)的右焦点,过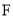 作该双曲线一条渐近线的垂线与两条渐近线交于
作该双曲线一条渐近线的垂线与两条渐近线交于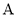 ,
,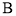 两点,
两点,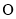 为坐标原点,
为坐标原点,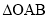 的面积为
的面积为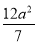 ,则该双曲线的离心率
,则该双曲线的离心率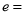 ( )
( )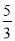 B.
B.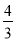 C.
C.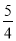 D.
D.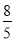
 中,
中, 平面
平面 ,
,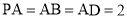 ,四边形
,四边形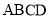 满足
满足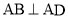 ,
,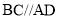 且
且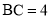 ,点
,点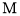 为
为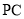 中点,点
中点,点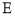 为
为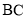 边上的动点,且
边上的动点,且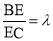 .
.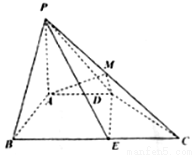
 求证:平面
求证:平面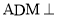 平面
平面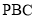 ;
;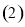 是否存在实数
是否存在实数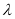 ,使得二面角
,使得二面角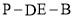 的余弦值为
的余弦值为 ?若存在,试求出实数
?若存在,试求出实数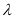 的值;若不存在,说明理由.
的值;若不存在,说明理由.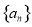 是公差不为
是公差不为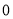 的等差数列,
的等差数列,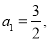 数列
数列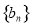 是等比数列,且
是等比数列,且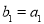 ,
,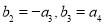 ,数列
,数列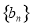 的前
的前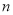 项和为
项和为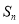 ,记点
,记点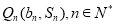 .
.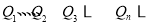 在同一直线
在同一直线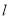 上,并求出直线
上,并求出直线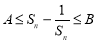 对
对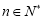 恒成立,求
恒成立,求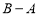 的最小值.
的最小值.