题目内容
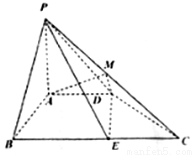
(本小题满分12分)如图,在四棱锥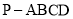 中,
中,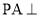 平面
平面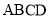 ,
,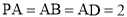 ,四边形
,四边形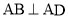 ,
,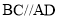 且
且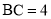 ,点
,点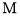 为
为 中点.
中点.
 求证:平面
求证:平面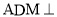 平面
平面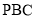 ;
;
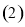 求点
求点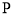 到平面
到平面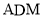 的距离.
的距离.
(1) 详见解析;(2)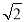
【解析】
试题分析:(1) 根据题中所证结论为:平面 平面
平面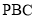 ,由面面垂直的判定定理转化为证明线面垂直,结合题所给条件不难想到取
,由面面垂直的判定定理转化为证明线面垂直,结合题所给条件不难想到取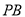 中点
中点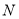 ,连结
,连结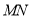 、
、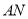 ,利用
,利用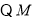 是
是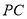 中点,由三角形中位线定理得:
中点,由三角形中位线定理得: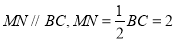 ,又
,又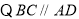 ,可得出四边形
,可得出四边形 为平行四边形,又由条件
为平行四边形,又由条件 ,易得:
,易得: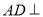 平面
平面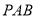 ,得:
,得: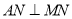 ;在
;在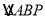 中有:
中有: ,易得:
,易得: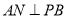 ,由线面垂直的判定定理得:
,由线面垂直的判定定理得: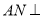 平面
平面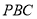 ,又由
,又由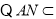 平面
平面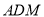 ,即可得:平面
,即可得:平面 平面
平面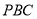 ;(2)由(1)知,
;(2)由(1)知,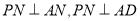 ,所以
,所以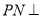 平面
平面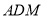 ,即点
,即点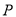 到平面
到平面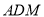 的距离为
的距离为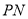 ,在
,在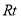 △
△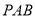 中,由
中,由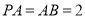 ,得
,得 ,所以
,所以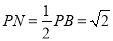 .
.
试题解析:(1) 取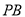 中点
中点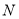 ,连结
,连结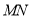 、
、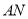
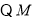 是
是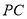 中点,
中点,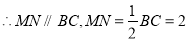 ,
,
又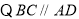 ,
,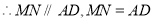 ,
, 四边形
四边形 为平行四边形
为平行四边形
 ,
, 平面
平面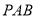 ,
, ,
,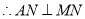
 ,
,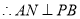 ,
,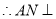 平面
平面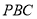 ,
,
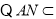 平面
平面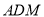 ,
, 平面
平面 平面
平面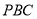 . (6分)
. (6分)
(2)由(1)知,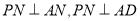 ,
,
所以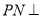 平面
平面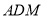 ,即点
,即点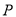 到平面
到平面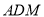 的距离为
的距离为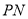 ,
,
在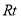 △
△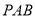 中,由
中,由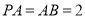 ,得
,得 ,所以
,所以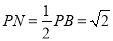 . (12分)
. (12分)
考点:1.线面以及面面的垂直;2.点到平面的距离

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 =( )
=( ) B.-
B.- D.2
D.2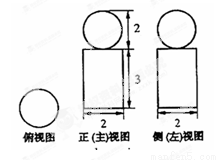
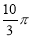 B.
B.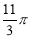 C.
C.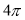 D.
D.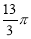
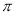 ;②图象关于直线
;②图象关于直线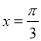 对称;③在
对称;③在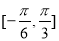 上是增函数”的一个函数是( )
上是增函数”的一个函数是( )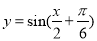 B.
B.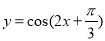
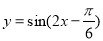 D.
D.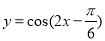
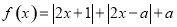 ,
,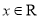 .
.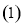 当
当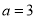 时,求不等式
时,求不等式 的解集;
的解集;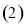 对任意
对任意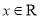 恒有
恒有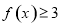 ,求实数
,求实数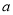 的取值范围.
的取值范围. 的焦点作倾斜角为
的焦点作倾斜角为 的直线
的直线 交抛物线于
交抛物线于 ,
, 两点,
两点, 为坐标原点,则
为坐标原点,则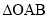 的面积为 .
的面积为 . ,
, 满足
满足 ,
, ,
, ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 且曲线
且曲线 、
、 与
与 所围成的封闭区域的面积为
所围成的封闭区域的面积为 ,则
,则 .
. 为正实数,则“
为正实数,则“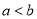 ”是“
”是“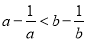 ”成立的( ).
”成立的( ).