题目内容
(本题满分16分)本题共3小题,第(1)小题4分,第(2)小题4分,第(3)小题8分.
已知数列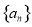 是公差不为
是公差不为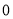 的等差数列,
的等差数列,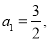 数列
数列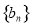 是等比数列,且
是等比数列,且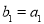 ,
,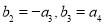 ,数列
,数列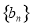 的前
的前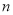 项和为
项和为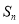 ,记点
,记点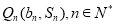 .
.
(1)求数列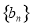 的通项公式;
的通项公式;
(2)证明:点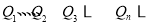 在同一直线
在同一直线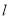 上,并求出直线
上,并求出直线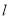 方程;
方程;
(3)若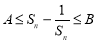 对
对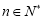 恒成立,求
恒成立,求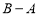 的最小值.
的最小值.
(1)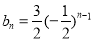 ,(2)
,(2)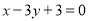 (3)
(3)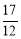
【解析】
试题分析:先根据题意列方程组,求出等比数列的公比及等差数列的公差,得到两数列的通项公式,第二步证明点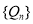 在一条直线上,只需证明
在一条直线上,只需证明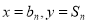 具有线性关系,满足直线方程,通过消元法可达目的,第三步恒成立问题,通过对
具有线性关系,满足直线方程,通过消元法可达目的,第三步恒成立问题,通过对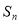 的单调性的讨论,研究
的单调性的讨论,研究 的单调性,从而求出
的单调性,从而求出 取值范围,进而找出的
取值范围,进而找出的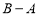 最小值.
最小值.
试题解析:(1)设等差数列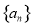 的公差为
的公差为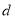 ,等比数列
,等比数列 的公比为
的公比为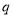 ,由题设可得
,由题设可得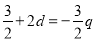 ....(1),
....(1),
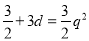 ...........(2),联立(1)(2)得方程组,解方程组得:
...........(2),联立(1)(2)得方程组,解方程组得: 或
或 ,因为数列
,因为数列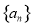 是公差不为0的等差数列,所以
是公差不为0的等差数列,所以 ,即
,即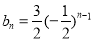
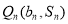 ,
,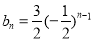 ,
,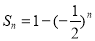 ,令
,令 ,两式消去
,两式消去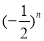 得
得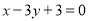 ,即点
,即点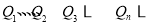 ,在同一条直线
,在同一条直线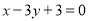 上。
上。
(3)由于  ,令
,令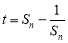 ,
,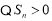 ,
, 随着
随着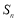 的增大而增大.
的增大而增大.
当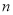 为奇数时,
为奇数时,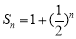 在奇数集上单调递减,
在奇数集上单调递减,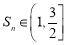 ,
,
当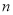 为偶数时,
为偶数时, 在偶数集上单调递增,
在偶数集上单调递增,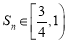 ,
,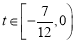
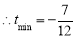 ,
, ,
, ,
, ,即
,即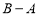 的最小值是
的最小值是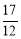
考点:1.等差数列和等比数列;2.证明一列点在直线上;3.与数列有关的综合问题;

练习册系列答案
相关题目
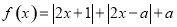 ,
,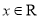 .
.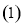 当
当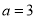 时,求不等式
时,求不等式 的解集;
的解集;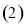 对任意
对任意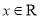 恒有
恒有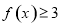 ,求实数
,求实数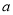 的取值范围.
的取值范围. ,
, 满足
满足 ,
, ,
, ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 展开式中
展开式中 的系数是________.
的系数是________.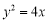 上的一点P到y轴的距离是4,则点P到该抛物线焦点的距离为( )
上的一点P到y轴的距离是4,则点P到该抛物线焦点的距离为( ) 为正实数,则“
为正实数,则“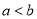 ”是“
”是“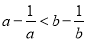 ”成立的( ).
”成立的( ). 门课程中各选修
门课程中各选修 门,则甲乙所选的课程中恰有
门,则甲乙所选的课程中恰有 门相同的选法有 种.
门相同的选法有 种.  中,角A,B。C的对边分别为
中,角A,B。C的对边分别为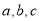 .已知
.已知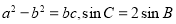 ,则角A为__________.
,则角A为__________. 恒成立,则实数
恒成立,则实数 的取值范围是
的取值范围是 B.
B. 
 D.
D. 