题目内容

某几何体的三视图如图，其中俯视图是一个半圆，内接一个直角边长是
2
的等腰三角形，侧视图下方是一个正方形，则该几何体的体积是
 
．
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由三视图可知：该几何体是一个组合体，上面是一个球的
1
4
，下面是一个直三棱柱．即可得出．
解答： 解：由三视图可知：该几何体是一个组合体，上面是一个球的
1
4
，下面是一个直三棱柱．
∴该几何体的体积V=
1
4
×
4
3
π×13+
1
2
×(
2
)2×2=2+
π
3
．
故答案为：2+
π
3
．
点评：本题考查了球与直三棱柱的体积计算公式、三视图，属于基础题．
练习册系列答案
相关题目
已知函数f（x）=
1
(x+1)2
．若f（x）+f（
1
x
）≥m恒成立，求m的最大值．
已知p：
3x+2
x-1
＞4，q：x2-6x+8-2m-m2＜0（m＜-1），
（1）若￢p是￢q的必要不充分条件，求m的取值范围；
（2）￢p是￢q的充分不必要条件，求m的取值范围．
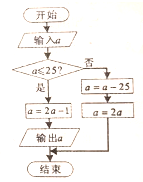某班有49位同学玩“数字接龙”游戏，具体规则按如图所示的程序框图执行（其中a为座位号），并以输出的值作为下一个输入的值，若第一次 输入的值为8，则第三次输出的值为（　　）
A、8B、15C、29D、36
圆（x-2）2+y2=4过点P（1，
3
）的切线方程是（　　）
A、x+
3
y-2=0
B、x+
3
y-4=0
C、x-
3
y+4=0
D、x-
3
y+2=0
已知
a
=（1，2），
a
.
b
=5，|
a
-
b
|=2
5
，则|
b
|=
 
．
已知变量x，y，满足约束条件
x+y-2≥0
y≤2
x-y≤0
，则z=2x-y的最大值为（　　）
A、2B、3C、4D、6
已知p：1g（x-1）≥1g（3-x），q：
1
x-2
≥1，则p是q的（　　）
A、充分而不必要条件
B、必要而不充分条件
C、充要条件
D、既不充分也不必要条件

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网