题目内容
9.若p:x(x-3)<0是q:2x-3<m的充分不必要条件,则实数m的取值范围是[3,+∞).分析 分别求出命题p,命题q的解集.由p是q的充分不必要条件,可得A?B,解出即可.
解答 解:命题p:x(x-3)<0,解的0<x<3,即解集A=(0,3)
命题q:2x-3<m的,解得,x<$\frac{m+3}{2}$,即解集B=(-∞,$\frac{m+3}{2}$)
∵p是q的充分不必要条件,
∴A?B,
∴$\frac{m+3}{2}$≥3,
解的m≥3,
则实数a的取值范围是[3,+∞),
故答案为:[3,+∞).
点评 本题考查了一元二次不等式的解法、充分必要条件的判定与应用,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
17.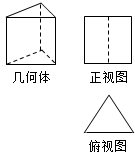 如图,水平放置的三棱柱的侧棱长和底边长均为4,且侧棱垂直于底面,正视图是边长为4的正方形,则三棱柱的左视图面积为( )
如图,水平放置的三棱柱的侧棱长和底边长均为4,且侧棱垂直于底面,正视图是边长为4的正方形,则三棱柱的左视图面积为( )
 如图,水平放置的三棱柱的侧棱长和底边长均为4,且侧棱垂直于底面,正视图是边长为4的正方形,则三棱柱的左视图面积为( )
如图,水平放置的三棱柱的侧棱长和底边长均为4,且侧棱垂直于底面,正视图是边长为4的正方形,则三棱柱的左视图面积为( )| A. | 8$\sqrt{3}$ | B. | 2$\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 4$\sqrt{3}$ |
4.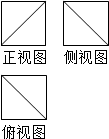 将某正方体工件进行切削,把它加工成一个体积尽可能大的新工件,新工件的三视图如图所示,则原工件材料的利用率为〔材料的利用率=$\frac{新工件的体积}{原工件的体积}$〕( )
将某正方体工件进行切削,把它加工成一个体积尽可能大的新工件,新工件的三视图如图所示,则原工件材料的利用率为〔材料的利用率=$\frac{新工件的体积}{原工件的体积}$〕( )
 将某正方体工件进行切削,把它加工成一个体积尽可能大的新工件,新工件的三视图如图所示,则原工件材料的利用率为〔材料的利用率=$\frac{新工件的体积}{原工件的体积}$〕( )
将某正方体工件进行切削,把它加工成一个体积尽可能大的新工件,新工件的三视图如图所示,则原工件材料的利用率为〔材料的利用率=$\frac{新工件的体积}{原工件的体积}$〕( )| A. | $\frac{7}{8}$ | B. | $\frac{6}{7}$ | C. | $\frac{5}{6}$ | D. | $\frac{4}{5}$ |
14.已知f(x)是定义在R上周期为2的奇函数,当x∈(0,1)时,f(x)=3x-1,则f(log35)=( )
| A. | $\frac{4}{5}$ | B. | -$\frac{4}{5}$ | C. | 4 | D. | $\frac{4}{9}$ |
1.已知f(x)+f(-x)=8,f(lg(log210))=5,则f(lg(lg2))=( )
| A. | -5 | B. | -1 | C. | 3 | D. | 4 |
18.有一组实验数据如表:
给出下列函数:①v=log${\;}_{\frac{1}{2}}$t;②v=$\sqrt{t}$;③v=($\frac{3}{2}$)t④y=$\frac{{t}^{2}-1}{2}$;
现准备用下列函数中的一个近似地表示这些数据满足的规律,其中最接近的一个是④(填序号).
| t | 1.99 | 3.0 | 4.0 | 5.1 | 6.12 |
| y | 1.50 | 4.04 | 7.50 | 12.00 | 18.01 |
现准备用下列函数中的一个近似地表示这些数据满足的规律,其中最接近的一个是④(填序号).
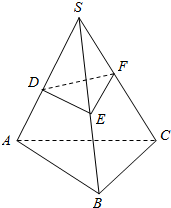 如图.D、E、F分别是三棱锥S-ABC,侧棱SA、SB、SC上的点.且SD:DA=SE:EB=CF:FS=2:1.那么过D、E、F的 平面截三棱锥S-ABC所得上下两部分体积的比为4:23.
如图.D、E、F分别是三棱锥S-ABC,侧棱SA、SB、SC上的点.且SD:DA=SE:EB=CF:FS=2:1.那么过D、E、F的 平面截三棱锥S-ABC所得上下两部分体积的比为4:23.