题目内容
设函数f（x）=
，则函数y=f（x）-（x2+1）的零点个数为 ．
|
考点：根的存在性及根的个数判断
专题：函数的性质及应用
分析：函数y=f（x）-（x2+1）的零点个数，即函数y=f（x）与函数y=x2+1图象交点的个数，在同一坐标系中画出函数y=f（x）与函数y=x2+1图象，数形结合，可得答案．
解答：
解：函数y=f（x）-（x2+1）的零点个数，
即函数y=f（x）与函数y=x2+1图象交点的个数，
在同一坐标系中画出函数y=f（x）与函数y=x2+1图象如下图所示：
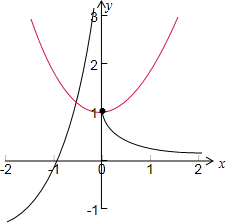
由图可得：出函数y=f（x）与函数y=x2+1图象有两个交点，
故函数y=f（x）-（x2+1）的零点个数为2个，
故答案为：2
即函数y=f（x）与函数y=x2+1图象交点的个数，
在同一坐标系中画出函数y=f（x）与函数y=x2+1图象如下图所示：
由图可得：出函数y=f（x）与函数y=x2+1图象有两个交点，
故函数y=f（x）-（x2+1）的零点个数为2个，
故答案为：2
点评：本题考查的知识点是函数的零点，其中将函数的零点的个数转化为函数图象交点的个数是解答的关键．
练习册系列答案
相关题目
已知等差数列{an}的前n项和为Sn，S9=-18，S13=-52，{bn}为等比数列，且b5=a5，b7=a7，则b15的值为（ ）
| A、64 | B、128 |
| C、-64 | D、-128 |
如图，在三棱锥S-ABC中，已知点E、F、G分别为棱SA、SC、BC的中点，过点E、F、G三点的平面与线段AB的交点为H．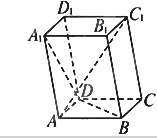
已知平行六面体ABCD-A1B1C1D1中，底面ABCD是边长为1的正方形．AA1=2，∠A1AB=∠A1AD=120°．在△ABC中，∠ABC=60°，AB=2，BC=6，在BC上任取一点D，使△ABD为钝角三角形的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
