题目内容
(本小题满分13分)
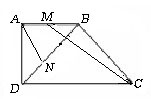
如图6所示,在直角坐标平面上的矩形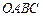 中,
中,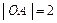 ,
,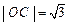 ,点
,点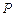 ,
,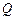 满足
满足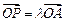 ,
,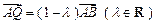 ,点
,点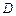 是
是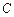 关于原点的对称点,直线
关于原点的对称点,直线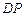 与
与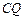 相交于点
相交于点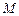 .
.
(Ⅰ)求点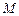 的轨迹方程;
的轨迹方程;
(Ⅱ)若过点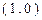 的直线与点
的直线与点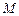 的轨迹相交于
的轨迹相交于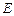 ,
,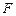 两点,求
两点,求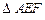 的面积的最大值.
的面积的最大值.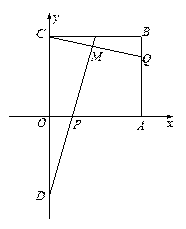
图6
如图6所示,在直角坐标平面上的矩形
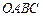 中,
中,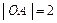 ,
,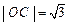 ,点
,点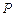 ,
,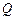 满足
满足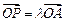 ,
,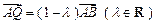 ,点
,点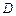 是
是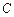 关于原点的对称点,直线
关于原点的对称点,直线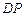 与
与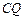 相交于点
相交于点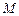 .
.(Ⅰ)求点
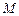 的轨迹方程;
的轨迹方程;(Ⅱ)若过点
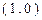 的直线与点
的直线与点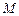 的轨迹相交于
的轨迹相交于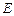 ,
,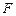 两点,求
两点,求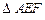 的面积的最大值.
的面积的最大值.
图6
(1)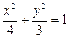 (2)
(2)
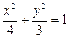 (2)
(2)
(Ⅰ)设点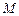 的坐标为
的坐标为 ,由图可知
,由图可知 ,
, ,
, ,
,
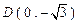 .
.
由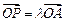 ,得点
,得点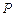 的坐标为
的坐标为 ;
;
由 ,得点
,得点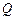 的坐标为
的坐标为
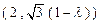 . ……
. …… 分
分
于是,当 时,直线
时,直线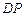 的方程为
的方程为
 , ……①
, ……①
直线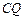 的方程为
的方程为 .……②
.……②
① ②,得
②,得 ,即
,即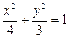 .
.
当 时,点
时,点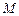 即为点
即为点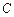 ,而点
,而点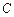 的坐标
的坐标 也满足上式.
也满足上式.
故点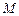 的轨迹方程为
的轨迹方程为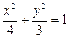 . ……
. …… 分
分
(Ⅱ)设过点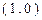 的直线
的直线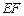 的方程为
的方程为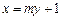 ,且设
,且设 ,
, .
.
由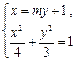 得
得 . ……③
. ……③
由于上述方程的判别式 ,所以
,所以 ,
, 是方程③的两根,
是方程③的两根,
根据求根公式,可得 .
.
又 ,所以
,所以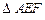 的面积
的面积 . ……
. ……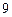 分
分
令
 ,则
,则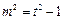 .
.
于是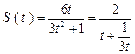 ,
,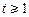 .
.
记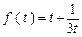 ,
,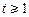 ,则
,则 .
.
因为当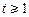 时,
时,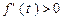 ,所以
,所以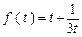 在
在 上单调递增.
上单调递增.
故当 时,
时, 取得最小值
取得最小值 ,此时
,此时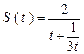 取得最大值
取得最大值 .
.
综上所述,当 时,即直线
时,即直线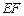 垂直于
垂直于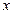 轴时,
轴时,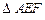 的面积取得最大值
的面积取得最大值 .
.
…… 分
分
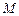 的坐标为
的坐标为 ,由图可知
,由图可知 ,
, ,
, ,
,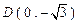 .
.由
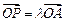 ,得点
,得点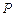 的坐标为
的坐标为 ;
;由
 ,得点
,得点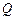 的坐标为
的坐标为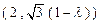 . ……
. ……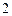 分
分于是,当
 时,直线
时,直线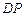 的方程为
的方程为 , ……①
, ……①直线
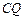 的方程为
的方程为 .……②
.……②①
 ②,得
②,得 ,即
,即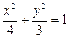 .
.当
 时,点
时,点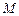 即为点
即为点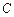 ,而点
,而点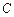 的坐标
的坐标 也满足上式.
也满足上式. 故点
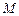 的轨迹方程为
的轨迹方程为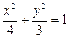 . ……
. …… 分
分(Ⅱ)设过点
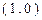 的直线
的直线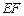 的方程为
的方程为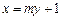 ,且设
,且设 ,
, .
.由
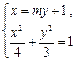 得
得 . ……③
. ……③由于上述方程的判别式
 ,所以
,所以 ,
, 是方程③的两根,
是方程③的两根,根据求根公式,可得
 .
.又
 ,所以
,所以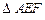 的面积
的面积 . ……
. ……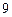 分
分令

 ,则
,则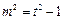 .
.于是
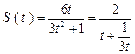 ,
,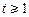 .
.记
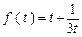 ,
,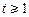 ,则
,则 .
.因为当
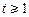 时,
时,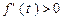 ,所以
,所以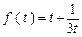 在
在 上单调递增.
上单调递增.故当
 时,
时, 取得最小值
取得最小值 ,此时
,此时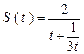 取得最大值
取得最大值 .
.综上所述,当
 时,即直线
时,即直线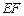 垂直于
垂直于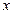 轴时,
轴时,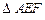 的面积取得最大值
的面积取得最大值 .
.……
 分
分
练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
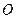 为坐标原点,
为坐标原点,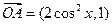 ,
,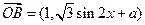 (
(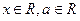 ,
,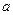 是常数),若
是常数),若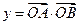
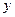 关于
关于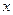 的函数关系式
的函数关系式 ;
; 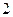 ,求
,求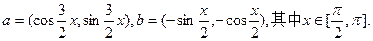
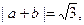 求x的值;
求x的值;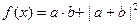 ,若
,若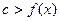 恒成立,求实数c的取值范围。
恒成立,求实数c的取值范围。
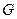








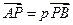
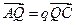

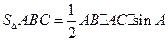 )
) ;(2)求
;(2)求 的取值范围
的取值范围 ,其中
,其中
 ∈R且
∈R且
 不共线,且
不共线,且 ,
,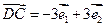 ,
, 共线
共线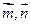 的夹角为
的夹角为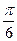 ,且
,且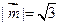 ,
,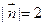 ,在
,在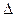 ABC中,
ABC中,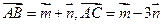 ,D为BC边的中点,则
,D为BC边的中点,则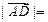 ( )
( )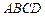 中,
中,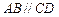 ,
,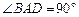 ,且
,且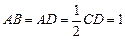 ,
,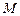 是
是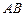 的中点,且
的中点,且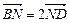 ,则
,则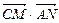 的值为( )
的值为( )