题目内容
设抛物线C:y2=4x的焦点为F,直线l过F且与C交于A,B两点,若|AF|=3|BF|,则|AB|等于( )
A、
| ||
B、
| ||
| C、3 | ||
D、
|
考点:抛物线的简单性质
专题:综合题,圆锥曲线的定义、性质与方程
分析:根据题意,可得抛物线焦点为F(1,0),由此设直线l方程为y=k(x-1),与抛物线方程联解消去x,设A(x1,y1),B(x2,y2),由根与系数的关系和|AF|=3|BF|,建立关于y1、y2和k的方程组,解之可得k值,即可求出|AB|.
解答:
解: ∵抛物线C方程为y2=4x,可得它的焦点为F(1,0),
∵抛物线C方程为y2=4x,可得它的焦点为F(1,0),
∴设直线l方程为y=k(x-1)
代入抛物线方程消去x,得
y2-y-k=0.
设A(x1,y1),B(x2,y2),
可得y1+y2=
,y1y2=-4…(*)
∵|AF|=3|BF|,
∴y1+3y2=0,可得y1=-3y2,代入(*)得-2y2=
且-3y22=-4,
消去y2得k2=3,解之得k=±
∴|AB|=
×
=
.
故选:B.
 ∵抛物线C方程为y2=4x,可得它的焦点为F(1,0),
∵抛物线C方程为y2=4x,可得它的焦点为F(1,0),∴设直线l方程为y=k(x-1)
代入抛物线方程消去x,得
| k |
| 4 |
设A(x1,y1),B(x2,y2),
可得y1+y2=
| 4 |
| k |
∵|AF|=3|BF|,
∴y1+3y2=0,可得y1=-3y2,代入(*)得-2y2=
| 4 |
| k |
消去y2得k2=3,解之得k=±
| 3 |
∴|AB|=
1+
|
|
| 16 |
| 3 |
故选:B.
点评:本题给出抛物线的焦点弦AB被焦点F分成1:3的两部分,求|AB|,着重考查了抛物线的标准方程、简单几何性质和直线与圆锥曲线的位置关系等知识,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
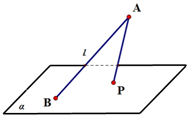 如图,点A是平面α外一定点,过A作平面α的斜线l,斜线l与平面α所成角为50°.若点P在平面α内运动,并使直线AP与l所成角为35°,则动点P的轨迹是( )
如图,点A是平面α外一定点,过A作平面α的斜线l,斜线l与平面α所成角为50°.若点P在平面α内运动,并使直线AP与l所成角为35°,则动点P的轨迹是( )| A、圆 | B、椭圆 |
| C、抛物线 | D、双曲线的一支 |
双曲线
-
=1(a>0,b>0)的一个焦点F到它的一条渐近线距离x满足a≤x≤3a,则该双曲线的离心率的取值范围为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、(
| ||||
B、(1,
| ||||
C、[2,
| ||||
D、[
|
已知函数f(x)=
sin(
x),为了得到函数g(x)=sin(
x)+cos(
x)的图象,只要将y=f(x)的图象( )
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
A、向右平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向左平移
|
 已知函数f(x)的定义域[-1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示,下列关于函数f(x)的命题其中错误的是( )
已知函数f(x)的定义域[-1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示,下列关于函数f(x)的命题其中错误的是( )| x | -1 | 0 | 2 | 4 | 5 |
| f (x) | 1 | 2 | 1.5 | 2 | 1 |
| A、函数f(x)的值域为[1,2] |
| B、函数f(x)在[0,2]上是减函数 |
| C、如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最大值为4 |
| D、当1<a<2时,函数y=f(x)-a最多有4个零点 |
已知一组变量x与y具有相关关系,对应值如下表:根据上表提供的数据,求出y关于x的线性回归方程为
=0.5x+1.25,那么表中t的值是( )
 |
| y |
| x | 3 | 4 | 5 | 6 |
| y | 3.5 | t | 4 | 4.5 |
| A、2 | B、3 | C、3.25 | D、3.5 |
已知log2a+log2b≥1,则3a+9b的最小值为( )
| A、6 | B、9 | C、16 | D、18 |