题目内容
19.已知几何体由两个直棱柱组合而成,其三视图和直观图如图所示.设两异面直线A1Q,PD所成的角为θ,则cosθ的值为$\frac{\sqrt{15}}{15}$.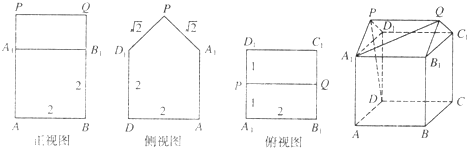
分析 先作出异面直线所成的角的平面角,即连接QC,再证明∠A1QC为异面直线A1Q、PD所成的角(或其补角),最后在△A1QC中计算此角的余弦值即可.
解答 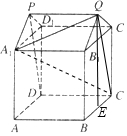 解:这个几何体的直观图如图,
解:这个几何体的直观图如图,
这个几何体可看成是由边长为2的正方体AC1及
底面边长为$\sqrt{2}$,$\sqrt{2}$,2,侧棱长为2的直三棱柱B1C1Q1-A1D1P的组合体,
由PQ∥CD,且PQ=CD,可知PD∥QC,
故∠A1QC为异面直线A1Q、PD所成的角(或其补角),
由题设知QA12=A1B12+B1Q2=22+2=6,
CA1=$\sqrt{3}$×2=2$\sqrt{3}$,取BC中点E,则QE⊥BC,
且QE=3,QC2=QE2+EC2=32+12=10,
由余弦定理,得cosθ=cos∠A1QC=$\frac{6+10-12}{2\sqrt{6}•\sqrt{10}}$=$\frac{\sqrt{15}}{15}$.
故答案为:$\frac{\sqrt{15}}{15}$.
点评 本题考查了空间想象能力,由三视图作出几何体的直观图,异面直线所成的角的定义及其求法.

练习册系列答案
相关题目
6.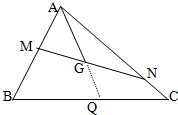 如图所示,已知点G是△ABC的重心,过点G作直线与AB,AC两边分别交于M,N两点,且$\overrightarrow{AM}$=x$\overrightarrow{AB}$,$\overrightarrow{AN}$=y$\overrightarrow{AC}$,则x+y的最小值为( )
如图所示,已知点G是△ABC的重心,过点G作直线与AB,AC两边分别交于M,N两点,且$\overrightarrow{AM}$=x$\overrightarrow{AB}$,$\overrightarrow{AN}$=y$\overrightarrow{AC}$,则x+y的最小值为( )
 如图所示,已知点G是△ABC的重心,过点G作直线与AB,AC两边分别交于M,N两点,且$\overrightarrow{AM}$=x$\overrightarrow{AB}$,$\overrightarrow{AN}$=y$\overrightarrow{AC}$,则x+y的最小值为( )
如图所示,已知点G是△ABC的重心,过点G作直线与AB,AC两边分别交于M,N两点,且$\overrightarrow{AM}$=x$\overrightarrow{AB}$,$\overrightarrow{AN}$=y$\overrightarrow{AC}$,则x+y的最小值为( )| A. | 2 | B. | $\frac{1}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{4}$ |
 如图,三棱锥的四个顶点P、A、B、C在同一个球面上,顶点P在平面ABC内的射影是H,若球心在直线PH上,则点H一定是△ABC的( )
如图,三棱锥的四个顶点P、A、B、C在同一个球面上,顶点P在平面ABC内的射影是H,若球心在直线PH上,则点H一定是△ABC的( )