题目内容
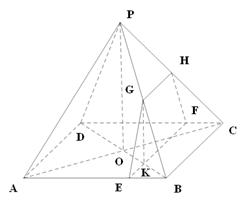
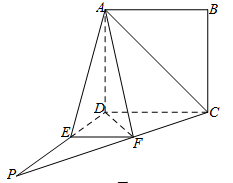
如图,四棱锥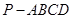 的底面边长为8的正方形,四条侧棱长均为
的底面边长为8的正方形,四条侧棱长均为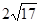 .点
.点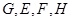 分别是棱
分别是棱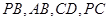 上共面的四点,平面
上共面的四点,平面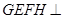 平面
平面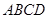 ,
,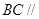 平面
平面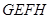 .
.
证明: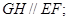
若 ,求四边形
,求四边形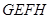 的面积.
的面积.
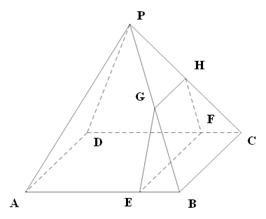
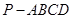 的底面边长为8的正方形,四条侧棱长均为
的底面边长为8的正方形,四条侧棱长均为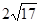 .点
.点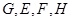 分别是棱
分别是棱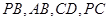 上共面的四点,平面
上共面的四点,平面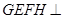 平面
平面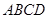 ,
,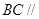 平面
平面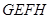 .
.证明:
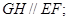
若
 ,求四边形
,求四边形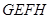 的面积.
的面积.
(1)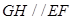 ;(2)
;(2)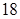 .
.
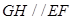 ;(2)
;(2)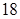 .
.试题分析:(1)要证线线平行,通过线面证明线线平行,再根据平行的传递性即可证明.因为
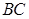 ∥平面
∥平面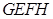 ,
,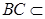 平面
平面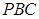 ,且平面
,且平面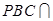 平面
平面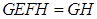 ,所以
,所以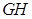 ∥
∥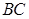 .同理可证
.同理可证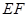 ∥
∥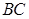 ,因此
,因此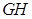 ∥
∥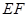 .(2)要求出四边形
.(2)要求出四边形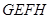 的面积,首先需要确定四边形的形状,求出四边形一些量的大小即可求出.连接
的面积,首先需要确定四边形的形状,求出四边形一些量的大小即可求出.连接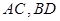 交于点
交于点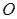 ,
,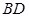 交
交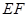 于点
于点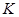 ,连接
,连接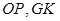 .因为
.因为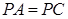 ,
,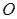 是
是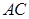 的中点,所以
的中点,所以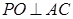 ,同理可得
,同理可得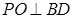 .又
.又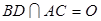 ,且
,且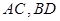 都在底面内,所以
都在底面内,所以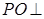 底面
底面 .又因为平面
.又因为平面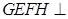 平面
平面 ,且
,且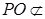 平面
平面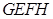 ,所以
,所以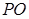 ∥平面
∥平面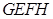 .因为平面
.因为平面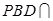 平面
平面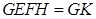 ,所以
,所以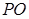 ∥
∥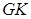 ,且
,且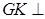 底面
底面 ,从而
,从而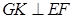 .所以
.所以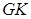 是梯形
是梯形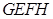 的高.由
的高.由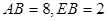 得
得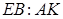 =
=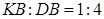 ,从而
,从而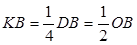 ,即
,即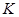 为
为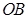 的中点.再由
的中点.再由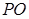 ∥
∥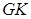 得
得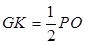 ,即
,即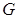 是
是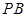 的中点,且
的中点,且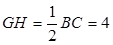 .由已知可得
.由已知可得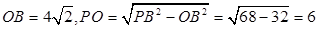 ,所以
,所以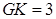 ,故四边形
,故四边形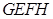 的面积
的面积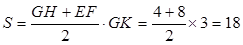 .
.(1)证明:因为
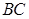 ∥平面
∥平面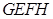 ,
,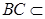 平面
平面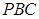 ,且平面
,且平面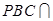 平面
平面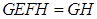 ,所以
,所以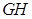 ∥
∥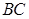 .同理可证
.同理可证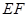 ∥
∥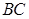 ,因此
,因此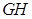 ∥
∥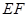 .
.
连接
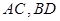 交于点
交于点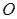 ,
,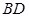 交
交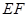 于点
于点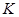 ,连接
,连接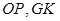 .因为
.因为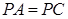 ,
,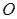 是
是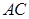 的中点,所以
的中点,所以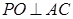 ,同理可得
,同理可得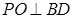 .又
.又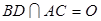 ,且
,且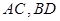 都在底面内,所以
都在底面内,所以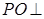 底面
底面 .又因为平面
.又因为平面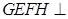 平面
平面 ,且
,且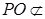 平面
平面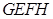 ,所以
,所以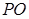 ∥平面
∥平面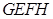 .因为平面
.因为平面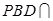 平面
平面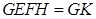 ,所以
,所以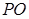 ∥
∥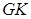 ,且
,且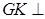 底面
底面 ,从而
,从而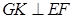 .所以
.所以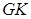 是梯形
是梯形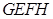 的高.由
的高.由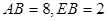 得
得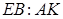 =
=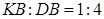 ,从而
,从而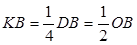 ,即
,即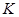 为
为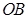 的中点.再由
的中点.再由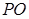 ∥
∥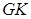 得
得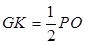 ,即
,即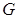 是
是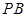 的中点,且
的中点,且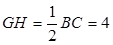 .由已知可得
.由已知可得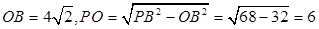 ,所以
,所以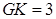 ,故四边形
,故四边形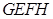 的面积
的面积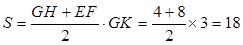 .
.
练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
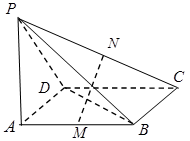
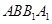 和
和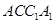 都为矩形。
都为矩形。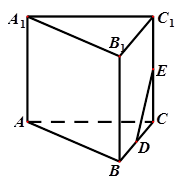
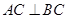 ,证明:直线
,证明:直线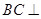 平面
平面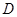 ,
,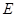 分别是线段
分别是线段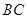 ,
,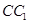 的中点,在线段
的中点,在线段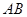 上是否存在一点
上是否存在一点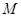 ,使直线
,使直线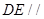 平面
平面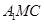 ?请证明你的结论。
?请证明你的结论。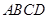 为正方形,
为正方形,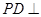 平面
平面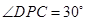 ,
,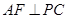 于点
于点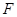 ,
,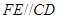 ,交
,交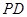 于点
于点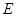 .
.
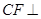 平面
平面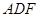 ;
;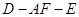 的余弦值.
的余弦值.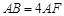 .
.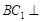 平面
平面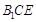 .
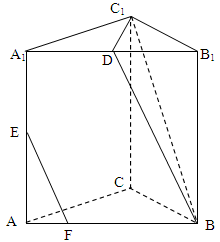
.
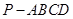 中,底面
中,底面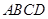 是边长为
是边长为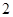 的正方形,侧面
的正方形,侧面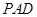
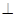
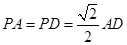 ,
,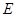 、
、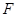 分别为
分别为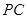 、
、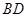 的中点.
的中点.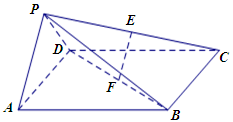
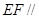 平面
平面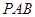
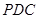 ;
; 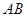 上是否存在点
上是否存在点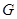 ,使得二面角
,使得二面角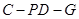 的余弦值为
的余弦值为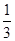 ?说明理由.
?说明理由.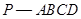 中,
中,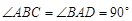 ,
,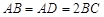 ,
,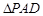 为正三角形,且平面
为正三角形,且平面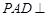 平面
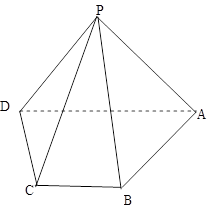
平面 .
.
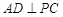 ;
;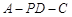 的余弦值.
的余弦值.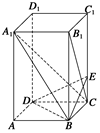 E是棱CC1上的点,且BE⊥B1C.
E是棱CC1上的点,且BE⊥B1C.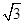 的球面上,若PA,PB,PC两两相互垂直,则球心到截面ABC的距离为________.
的球面上,若PA,PB,PC两两相互垂直,则球心到截面ABC的距离为________.