题目内容
如图所示,已知长方体ABCD—A1B1C1D1中,AB=BC=2,AA1=4,
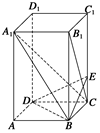 E是棱CC1上的点,且BE⊥B1C.
E是棱CC1上的点,且BE⊥B1C.
(1)求CE的长;
(2)求证:A1C⊥平面BED;
(3)求A1B与平面BDE所成角的正弦值.
 E是棱CC1上的点,且BE⊥B1C.
E是棱CC1上的点,且BE⊥B1C.(1)求CE的长;
(2)求证:A1C⊥平面BED;
(3)求A1B与平面BDE所成角的正弦值.
(1) CE="1" (2)证明略(3)A1B与平面BDE所成角的正弦值为

(1) 如图所示,以D为原点,DA、DC、DD1所在直线分别为x、y、z轴建立空间直角坐标系D—xyz.

∴D(0,0,0),A(2,0,0),B(2,2,0),
C(0,2,0),A1(2,0,4),
B1(2,2,4),C1(0,2,4),D1(0,0,4).
设E点坐标为(0,2,t),则 =(-2,0,t),
=(-2,0,t), =(-2,0,-4).
=(-2,0,-4).
∵BE⊥B1C,
∴ ·
· =4+0-4t=0.∴t=1,故CE=1.
=4+0-4t=0.∴t=1,故CE=1.
(2)由(1)得,E(0,2,1), =(-2,0,1),
=(-2,0,1),
又 =(-2,2,-4),
=(-2,2,-4), =(2,2,0),
=(2,2,0),
∴ ·
· =4+0-4=0,
=4+0-4=0,
且 ·
· =-4+4+0=0.
=-4+4+0=0.
∴ ⊥
⊥ 且
且 ⊥
⊥ ,即A1C⊥DB,A1C⊥BE,
,即A1C⊥DB,A1C⊥BE,
又∵DB∩BE=B,∴A1C⊥平面BDE.
即A1C⊥平面BED.
(3) 由(2)知 =(-2,2,-4)是平面BDE的一个法向量.又
=(-2,2,-4)是平面BDE的一个法向量.又 =(0,2,-4),
=(0,2,-4),
∴cos〈 ,
, 〉=
〉= =
= .
.
∴A1B与平面BDE所成角的正弦值为 .
.

∴D(0,0,0),A(2,0,0),B(2,2,0),
C(0,2,0),A1(2,0,4),
B1(2,2,4),C1(0,2,4),D1(0,0,4).
设E点坐标为(0,2,t),则
 =(-2,0,t),
=(-2,0,t), =(-2,0,-4).
=(-2,0,-4).∵BE⊥B1C,
∴
 ·
· =4+0-4t=0.∴t=1,故CE=1.
=4+0-4t=0.∴t=1,故CE=1.(2)由(1)得,E(0,2,1),
 =(-2,0,1),
=(-2,0,1),又
 =(-2,2,-4),
=(-2,2,-4), =(2,2,0),
=(2,2,0),∴
 ·
· =4+0-4=0,
=4+0-4=0,且
 ·
· =-4+4+0=0.
=-4+4+0=0.∴
 ⊥
⊥ 且
且 ⊥
⊥ ,即A1C⊥DB,A1C⊥BE,
,即A1C⊥DB,A1C⊥BE,又∵DB∩BE=B,∴A1C⊥平面BDE.
即A1C⊥平面BED.
(3) 由(2)知
 =(-2,2,-4)是平面BDE的一个法向量.又
=(-2,2,-4)是平面BDE的一个法向量.又 =(0,2,-4),
=(0,2,-4),∴cos〈
 ,
, 〉=
〉= =
= .
.∴A1B与平面BDE所成角的正弦值为
 .
.
练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
 中,
中, ,底面
,底面 为直角梯形,
为直角梯形, ,点
,点 在棱
在棱 上,且
上,且 .
. 所成的角;
所成的角; 平面
平面 ;
; 的余弦值.
的余弦值.
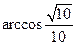 ,求BD的长度.(15分)
,求BD的长度.(15分)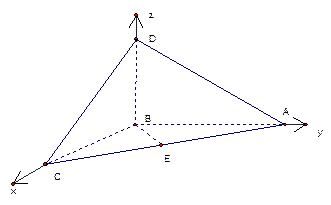
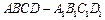 的棱长为2,
的棱长为2,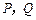 分别是
分别是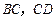 上的动点,且
上的动点,且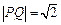 ,确定
,确定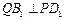 .
.
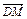 ,
,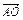 〉.
〉.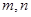 是两条不同的直线,
是两条不同的直线, 是两个不重合的平面,给定下列四个命题:
是两个不重合的平面,给定下列四个命题: ,
,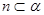 ,则
,则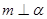 ;
;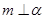 ,
,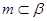 ,则
,则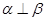 ;
; ,则
,则 ;
;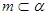 ,
, ,
, ,则
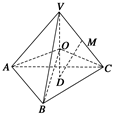
,则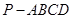 的底面边长为8的正方形,四条侧棱长均为
的底面边长为8的正方形,四条侧棱长均为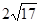 .点
.点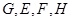 分别是棱
分别是棱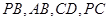 上共面的四点,平面
上共面的四点,平面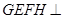 平面
平面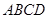 ,
,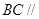 平面
平面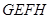 .
.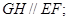
 ,求四边形
,求四边形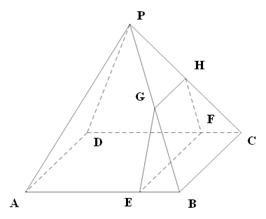
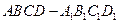 的棱长是
的棱长是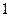 ,则直线
,则直线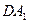 与
与 间的距离为 。
间的距离为 。