题目内容
如图,已知椭圆的中心在坐标原点,焦点F1,F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M,|MA1|∶|A1F1|=2∶1.
(Ⅰ)求椭圆的方程;
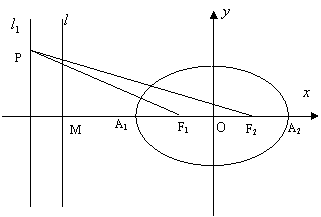
(Ⅱ)若直线l1:x=m(|m|>1),P为l1上的动点,使∠F1PF2最大的点P记为Q,求点Q的坐标(用m表示).
(Ⅰ)求椭圆的方程;

(Ⅱ)若直线l1:x=m(|m|>1),P为l1上的动点,使∠F1PF2最大的点P记为Q,求点Q的坐标(用m表示).
:(I)设椭圆方程为 (
( ),半焦距为c, 则
),半焦距为c, 则 ,
, ,
,
由题意,得 , 解得
, 解得 ,故椭圆方程为
,故椭圆方程为
(II)设P(
当 时,
时,
当 时,
时,  ,
, 只需求
只需求 的最大值即可.
的最大值即可.
直线 的斜率
的斜率 ,直线
,直线 的斜率
的斜率


当且仅当 =
= 时,
时, 最大,
最大,
 (
( ),半焦距为c, 则
),半焦距为c, 则 ,
, ,
,由题意,得
 , 解得
, 解得 ,故椭圆方程为
,故椭圆方程为
(II)设P(

当
 时,
时,
当
 时,
时,  ,
, 只需求
只需求 的最大值即可.
的最大值即可.直线
 的斜率
的斜率 ,直线
,直线 的斜率
的斜率


当且仅当
 =
= 时,
时, 最大,
最大,:(1)待定系数法;(2)利用夹角公式将∠F1PF2的正切值用y0表示出来,利用基本不等式求其最值.

练习册系列答案
相关题目
 ,过抛物线C上一点P(x0,y0)(x 0≠0)作斜率为k1,k2的两条直线分别交抛物线C于A(x1,y1)B(x2,y2)两点(P,A,B三点互不相同),且满足
,过抛物线C上一点P(x0,y0)(x 0≠0)作斜率为k1,k2的两条直线分别交抛物线C于A(x1,y1)B(x2,y2)两点(P,A,B三点互不相同),且满足 .
. ,证明线段PM的中点在y轴上;
,证明线段PM的中点在y轴上; =1时,若点P的坐标为(1,-1),求∠PAB为钝角时点A的纵坐标
=1时,若点P的坐标为(1,-1),求∠PAB为钝角时点A的纵坐标 的取值范围.
的取值范围. :
: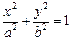 (
(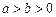 ),其左、右焦点分别为
),其左、右焦点分别为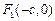 、
、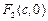 ,且
,且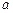 、
、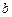 、
、 成等比数列.
成等比数列.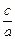 的值.
的值.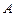 、
、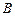 ,求证:
,求证: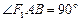 .
.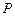 为椭圆
为椭圆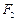 、
、 ,使
,使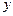 轴的交点
轴的交点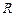 满足
满足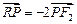 ?若存在,求直线
?若存在,求直线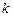 ;若不存在,请说明理由.
;若不存在,请说明理由.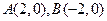 ,
,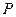 是平面内一动点,直线
是平面内一动点,直线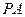 、
、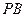 斜率之积为
斜率之积为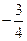 。
。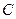 的方程;
的方程;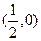 作直线
作直线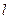 与轨迹
与轨迹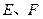 两点,线段
两点,线段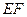 的中点为
的中点为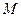 ,求直线
,求直线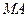 的斜率
的斜率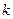 的取值范围。
的取值范围。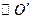 过定点
过定点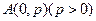 ,圆心
,圆心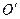 在抛物线
在抛物线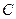 :
: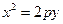 上运动,
上运动,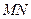 为圆
为圆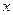 轴上所截得的弦.
轴上所截得的弦.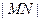 是否有变化?并证明你的结论;
是否有变化?并证明你的结论;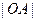 是
是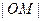 与
与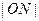 的等差中项时,
的等差中项时,
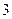 的线段
的线段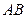 的端点
的端点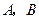 在抛物线
在抛物线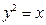 上移动,求
上移动,求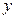 轴距离的最小值,并求出此时
轴距离的最小值,并求出此时

 B
B 
 D
D 
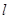 经过二、三、四象限,
经过二、三、四象限,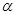 ,斜率为k,则 ( ).
,斜率为k,则 ( ).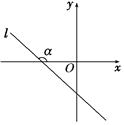
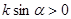
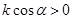
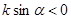
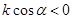
 的取值范围是( )
的取值范围是( ) ,2]
,2] ]
]