题目内容
抛物线C的方程为 ,过抛物线C上一点P(x0,y0)(x 0≠0)作斜率为k1,k2的两条直线分别交抛物线C于A(x1,y1)B(x2,y2)两点(P,A,B三点互不相同),且满足
,过抛物线C上一点P(x0,y0)(x 0≠0)作斜率为k1,k2的两条直线分别交抛物线C于A(x1,y1)B(x2,y2)两点(P,A,B三点互不相同),且满足 .
.
(Ⅰ)求抛物线C的焦点坐标和准线方程;
(Ⅱ)设直线AB上一点M,满足 ,证明线段PM的中点在y轴上;
,证明线段PM的中点在y轴上;
(Ⅲ)当 =1时,若点P的坐标为(1,-1),求∠PAB为钝角时点A的纵坐标
=1时,若点P的坐标为(1,-1),求∠PAB为钝角时点A的纵坐标 的取值范围.
的取值范围.
 ,过抛物线C上一点P(x0,y0)(x 0≠0)作斜率为k1,k2的两条直线分别交抛物线C于A(x1,y1)B(x2,y2)两点(P,A,B三点互不相同),且满足
,过抛物线C上一点P(x0,y0)(x 0≠0)作斜率为k1,k2的两条直线分别交抛物线C于A(x1,y1)B(x2,y2)两点(P,A,B三点互不相同),且满足 .
.(Ⅰ)求抛物线C的焦点坐标和准线方程;
(Ⅱ)设直线AB上一点M,满足
 ,证明线段PM的中点在y轴上;
,证明线段PM的中点在y轴上;(Ⅲ)当
 =1时,若点P的坐标为(1,-1),求∠PAB为钝角时点A的纵坐标
=1时,若点P的坐标为(1,-1),求∠PAB为钝角时点A的纵坐标 的取值范围.
的取值范围.(Ⅰ)由抛物线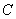 的方程
的方程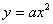 (
(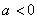 )得,焦点坐标为
)得,焦点坐标为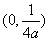 ,准线方程为
,准线方程为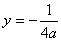 .
.
(Ⅱ)证明:设直线 的方程为
的方程为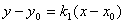 ,直线
,直线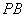 的方程为
的方程为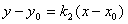 .
.
点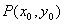 和点
和点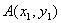 的坐标是方程组
的坐标是方程组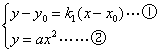 的解.将②式代入①式得
的解.将②式代入①式得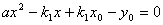 ,于是
,于是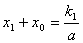 ,故
,故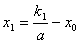 ③
③
又点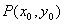 和点
和点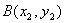 的坐标是方程组
的坐标是方程组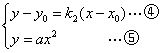 的解.将⑤式代入④式得
的解.将⑤式代入④式得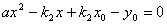 .于是
.于是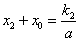 ,故
,故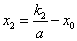 .
.
由已知得,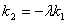 ,则
,则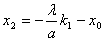 . ⑥
. ⑥
设点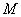 的坐标为
的坐标为 ,由
,由 ,则
,则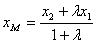 .
.
将③式和⑥式代入上式得 ,即
,即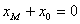 .
.
∴线段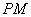 的中点在
的中点在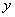 轴上.
轴上.
(Ⅲ)因为点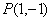 在抛物线
在抛物线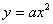 上,所以
上,所以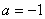 ,抛物线方程为
,抛物线方程为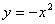 .
.
由③式知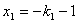 ,代入
,代入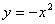 得
得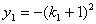 .
.
将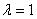 代入⑥式得
代入⑥式得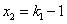 ,代入
,代入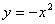 得
得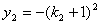 .
.
因此,直线 、
、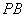 分别与抛物线
分别与抛物线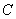 的交点
的交点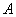 、
、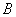 的坐标为
的坐标为
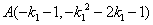 ,
,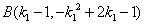 .
.
于是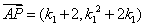 ,
,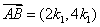 ,
,
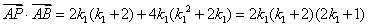 .
.
因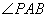 为钝角且
为钝角且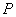 、
、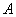 、
、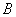 三点互不相同,故必有
三点互不相同,故必有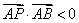 .
.
求得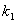 的取值范围是
的取值范围是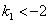 或
或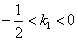 .又点
.又点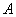 的纵坐标
的纵坐标 满足
满足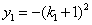 ,故当
,故当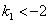 时,
时,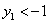 ;当
;当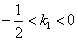 时,
时,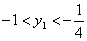 .即
.即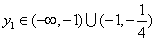
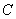 的方程
的方程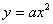 (
(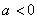 )得,焦点坐标为
)得,焦点坐标为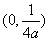 ,准线方程为
,准线方程为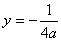 .
.(Ⅱ)证明:设直线
 的方程为
的方程为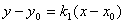 ,直线
,直线 的方程为
的方程为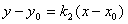 .
.点
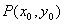 和点
和点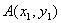 的坐标是方程组
的坐标是方程组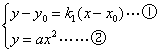 的解.将②式代入①式得
的解.将②式代入①式得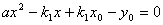 ,于是
,于是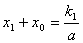 ,故
,故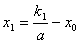 ③
③又点
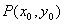 和点
和点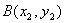 的坐标是方程组
的坐标是方程组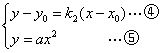 的解.将⑤式代入④式得
的解.将⑤式代入④式得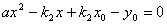 .于是
.于是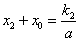 ,故
,故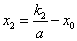 .
.由已知得,
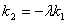 ,则
,则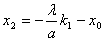 . ⑥
. ⑥设点
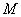 的坐标为
的坐标为 ,由
,由 ,则
,则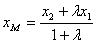 .
.将③式和⑥式代入上式得
 ,即
,即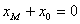 .
.∴线段
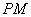 的中点在
的中点在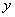 轴上.
轴上.(Ⅲ)因为点
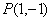 在抛物线
在抛物线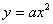 上,所以
上,所以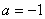 ,抛物线方程为
,抛物线方程为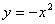 .
.由③式知
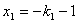 ,代入
,代入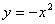 得
得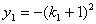 .
.将
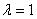 代入⑥式得
代入⑥式得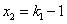 ,代入
,代入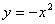 得
得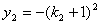 .
.因此,直线
 、
、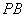 分别与抛物线
分别与抛物线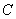 的交点
的交点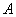 、
、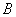 的坐标为
的坐标为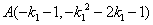 ,
,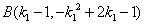 .
.于是
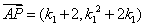 ,
,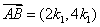 ,
,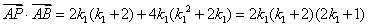 .
.因
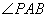 为钝角且
为钝角且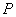 、
、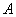 、
、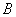 三点互不相同,故必有
三点互不相同,故必有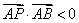 .
.求得
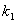 的取值范围是
的取值范围是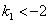 或
或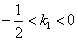 .又点
.又点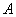 的纵坐标
的纵坐标 满足
满足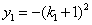 ,故当
,故当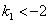 时,
时,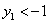 ;当
;当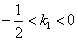 时,
时,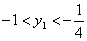 .即
.即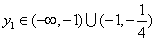
将直线方程和抛物线方程组成的方程组转化为一元二次方程,用韦达定理来求解.点评:解析几何解题思维方法比较简单,但对运算能力的要求比较高,平时练习要注意提高自己的运算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
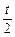 ,
,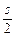 )对称.
)对称.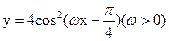 的图象与直线y=3在y轴右侧的交点按横坐标从小到大依次为P1,P2,P3,…,若
的图象与直线y=3在y轴右侧的交点按横坐标从小到大依次为P1,P2,P3,…,若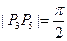 ,则
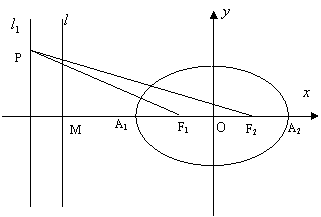
,则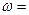 。
。
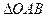
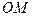

 若直线
若直线 :
: 与线段PQ的延长线相交,则
与线段PQ的延长线相交,则 的取值范围是 .
的取值范围是 . ∪
∪

 的右焦点为
的右焦点为 ,则该双曲线的渐近线方程为 .
,则该双曲线的渐近线方程为 .