题目内容
已知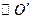 过定点
过定点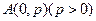 ,圆心
,圆心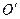 在抛物线
在抛物线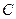 :
: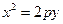 上运动,
上运动,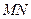 为圆
为圆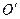 在
在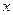 轴上所截得的弦.
轴上所截得的弦.
⑴当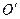 点运动时,
点运动时,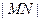 是否有变化?并证明你的结论;
是否有变化?并证明你的结论;
⑵当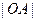 是
是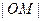 与
与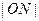 的等差中项时,
的等差中项时,
试判断抛物线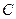 的准线与圆
的准线与圆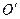 的位置关系,
的位置关系,
并说明理由。

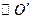 过定点
过定点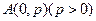 ,圆心
,圆心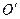 在抛物线
在抛物线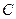 :
: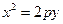 上运动,
上运动,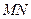 为圆
为圆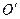 在
在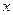 轴上所截得的弦.
轴上所截得的弦.⑴当
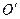 点运动时,
点运动时,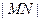 是否有变化?并证明你的结论;
是否有变化?并证明你的结论;⑵当
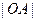 是
是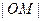 与
与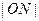 的等差中项时,
的等差中项时,试判断抛物线
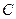 的准线与圆
的准线与圆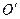 的位置关系,
的位置关系,并说明理由。

(1)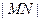 不变化,为定值
不变化,为定值 (2)抛物线
(2)抛物线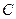 的准线与圆
的准线与圆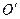 相交
相交
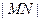 不变化,为定值
不变化,为定值 (2)抛物线
(2)抛物线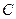 的准线与圆
的准线与圆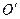 相交
相交解:(1)设 则
则
则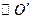 的半径
的半径 ……(2分)
……(2分)
⊙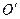 的方程为
的方程为
令 ,并把
,并把 代入得
代入得 , ……(3分)
, ……(3分)
解得 ,∴
,∴ , ……(5分)
, ……(5分)
∴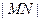 不变化,为定值
不变化,为定值 . ……(6分)
. ……(6分)
(2)∵ ,而
,而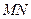 的中点横坐标为
的中点横坐标为 ,
,
∴不妨设 ,则由
,则由 有
有
 ,
,
∴ ,即
,即 ……(9分)
……(9分)
圆心到抛物线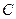 的准线
的准线 的距离
的距离 ,
,
而圆的半径为 ……(11分)
……(11分)

 则
则
则
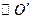 的半径
的半径 ……(2分)
……(2分)⊙
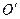 的方程为
的方程为
令
 ,并把
,并把 代入得
代入得 , ……(3分)
, ……(3分)解得
 ,∴
,∴ , ……(5分)
, ……(5分)∴
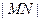 不变化,为定值
不变化,为定值 . ……(6分)
. ……(6分)(2)∵
 ,而
,而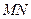 的中点横坐标为
的中点横坐标为 ,
,∴不妨设
 ,则由
,则由 有
有 ,
,∴
 ,即
,即 ……(9分)
……(9分)圆心到抛物线
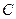 的准线
的准线 的距离
的距离 ,
,而圆的半径为
 ……(11分)
……(11分)

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
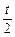 ,
,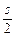 )对称.
)对称.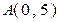 为圆心、双曲线
为圆心、双曲线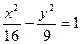 的渐近线为切线的圆的标准方程是____ __.
的渐近线为切线的圆的标准方程是____ __.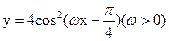 的图象与直线y=3在y轴右侧的交点按横坐标从小到大依次为P1,P2,P3,…,若
的图象与直线y=3在y轴右侧的交点按横坐标从小到大依次为P1,P2,P3,…,若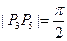 ,则
,则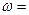 。
。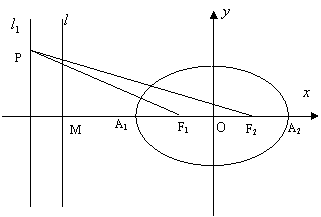
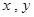 满足等式
满足等式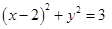 ,那么
,那么 的最大值为______.
的最大值为______.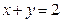
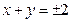
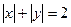
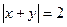
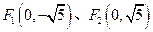 ,动点
,动点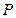 满足条件:
满足条件: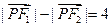 ,设点
,设点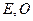 为坐标原点。
为坐标原点。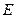 的方程;
的方程;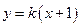 与曲线
与曲线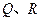 ,求
,求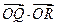 的取值范围;
的取值范围;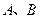 两点分别在直线
两点分别在直线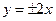 上,若
上,若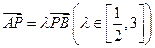 ,记
,记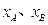 分别为
分别为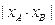 的最小值。
的最小值。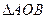 面积的最大值。
面积的最大值。