题目内容
若|
|=1，|
|=2，且
，
的夹角为120°，则|
+
|的值（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| A、1 | ||
B、
| ||
C、
| ||
| D、2 |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：根据向量的平方等于模的平方，利用数量积定义和数量积的性质即可得出．
解答：
解：∵|
|=1，|
|=2，且
，
的夹角为120°，
∴
2=1，
2=4，
•
=-1，
∴|
+
|2=（
+
）2=
2+
2-2
•
=1+4-2=3，
故|
+
|=
，
故选：B
| a |
| b |
| a |
| b |
∴
| a |
| b |
| a |
| b |
∴|
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
故|
| a |
| b |
| 3 |
故选：B
点评：本题考查了数量积定义和数量积的性质，属于基础题．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
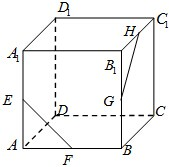如图，在正方体ABCDA1B1C1D1中，E、F、G、H分别为AA1、AB、BB1、BC1的中点，则异面直线EF与GH所成的角等于（ ）| A、30° | B、45° |
| C、60° | D、90° |
设f（x）=
，则
f（x）dx的值为（ ）
|
| ∫ | 2 0 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知定义域为R的奇函数f（x）的导函数为f′（x），当x≠0时，f′（x）+
＞0，若a=
f（
），b=-2f（-2），c=ln
f（ln2），则下列关于a，b，c的大小关系正确的是（ ）
| f(x) |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| A、a＞b＞c |
| B、b＞a＞c |
| C、c＞b＞a |
| D、a＞c＞b |
若a=21.2，b=(
)-0.8，c=2log52，则（ ）
| 1 |
| 2 |
| A、c＜b＜a |
| B、b＜a＜c |
| C、c＜a＜b |
| D、b＜c＜a |
根据如图所示的程序框图，若输出的结果T=600，则图中横线上应填（ ）
| A、48 | B、50 | C、52 | D、54 |
下列函数在（1，+∞）上是增函数的是（ ）
| A、y=-2x | ||
B、y=log
| ||
| C、y=-（x-1） | ||
| D、y=|x-1| |
已知g（x）=ax+2，f（x）=
，对?x1∈[-1，3]，?x0∈[-1，3]，使g（x1）=f（x0）恒成立，则a的取值范围是（ ）
|
| A、a≥-1 | ||
B、-1≤a≤
| ||
C、0＜a≤
| ||
D、a≤
|