题目内容
已知中心在坐标原点,以坐标轴为对称轴的椭圆C过点Q(1,
),且点Q在x轴的射影恰为该椭圆的一个焦点F1.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过椭圆C的一个焦点F作与x轴不垂直的任意直线l交椭圆于A、B两点,线段AB的垂直平分线交x轴于点M,则
是否为定值,若为定值,求出该定值,若不为定值,说明理由.
| 3 |
| 2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)过椭圆C的一个焦点F作与x轴不垂直的任意直线l交椭圆于A、B两点,线段AB的垂直平分线交x轴于点M,则
| |AB| |
| |FM| |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(I)由已知条件设椭圆方程为
+
=1,把Q(1,
)代入,能求出椭圆C的方程.
(II)“过椭圆
+
=1的一个焦点F作与x轴不垂直的任意直线l交椭圆于A、B两点,线段AB的垂直平分线交x轴于点M,则
为定值,且定值是4”.利用直线和椭圆的位置关系能够进行证明.
| x2 |
| a2 |
| y2 |
| a2-1 |
| 3 |
| 2 |
(II)“过椭圆
| x2 |
| 4 |
| y2 |
| 3 |
| |AB| |
| |FM| |
解答:
解:(I)∵中心在坐标原点,以坐标轴为对称轴的椭圆C过点Q(1,
),
且点Q在x轴的射影恰为该椭圆的一个焦点F1,
∴设椭圆方程为
+
=1,
把Q(1,
)代入,得:
+
=1,
整理,得4a4-17a2-4=0,
解得a2=4,或a2=
,
∴椭圆C的方程为
+
=1…(4分)
(II)“过椭圆
+
=1的一个焦点F作与x轴不垂直的任意直线l交椭圆于A、B两点,
线段AB的垂直平分线交x轴于点M,则
为定值,且定值是4”…(5分)
证明如下:
由于l与x轴不垂直,可设直线l的方程为y=k(x-1)
①当k≠0时,由
得(3+4k2)x2-8k2x+4k2-12=0.
依题意l与C有两个交点A、B,所以△>0.
设A(x1,y1),B(x2,y2),
则x1+x2=
,x1x2=
,y1+y2=k(x1+x2-2)=
,
所以线段AB的中点P的坐标为(
,
),…(7分)
AB的垂直平分线MP的方程为:y+
=-
(x-
).
令y=0,解得x=
,即M(
,0),
所以|F1M|=
.…(9分)
又|AB|=
=
=
•
=
•
=
,…(10分)
所以
=4.…(11分)
②k=0时,易得结论成立.
综上所述,结论成立.^…(12分)
| 3 |
| 2 |
且点Q在x轴的射影恰为该椭圆的一个焦点F1,
∴设椭圆方程为
| x2 |
| a2 |
| y2 |
| a2-1 |
把Q(1,
| 3 |
| 2 |
| 1 |
| a2 |
| ||
| a2-1 |
整理,得4a4-17a2-4=0,
解得a2=4,或a2=
| 1 |
| 4 |
∴椭圆C的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(II)“过椭圆
| x2 |
| 4 |
| y2 |
| 3 |
线段AB的垂直平分线交x轴于点M,则
| |AB| |
| |FM| |
证明如下:
由于l与x轴不垂直,可设直线l的方程为y=k(x-1)
①当k≠0时,由
|
依题意l与C有两个交点A、B,所以△>0.
设A(x1,y1),B(x2,y2),
则x1+x2=
| 8k2 |
| 3+4k2 |
| 4k2-12 |
| 3+4k2 |
| -6k |
| 3+4k2 |
所以线段AB的中点P的坐标为(
| 4k2 |
| 3+4k2 |
| -3k |
| 3+4k2 |
AB的垂直平分线MP的方程为:y+
| 3k |
| 3+4k2 |
| 1 |
| k |
| 4k2 |
| 3+4k2 |
令y=0,解得x=
| k2 |
| 3+4k2 |
| k2 |
| 3+4k2 |
所以|F1M|=
| 3(1+k2) |
| 3+4k2 |
又|AB|=
| (x1-x2)2+(y1-y2)2 |
| (1+k2)(x1-x2)2 |
| 1+k2 |
| (x1+x2)2-4x1x2 |
=
| 1+k2 |
(
|
| 12(1+k2) |
| 3+4k2 |
所以
| |AB| |
| |F1M| |
②k=0时,易得结论成立.
综上所述,结论成立.^…(12分)
点评:本题考查椭圆方程的求法,考查两条线段长的比值是否为定值的判断与证明,解题时要认真审题,注意待定系数法的合理运用.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
若随机变量ξ~B(n,P),且Eξ=6,Dξ=3,则P(ξ=1)的值为( )
| A、3•2-2 |
| B、3•2-10 |
| C、2-4 |
| D、2-8 |
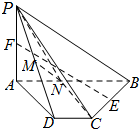 如图所示,四棱锥P-ABCD中,PA⊥面ABCD,AB∥CD,∠ABC=90°,AP=BC=2,AB=3,CD=1,E、F、M分别是BC、PA、PD的中点.
如图所示,四棱锥P-ABCD中,PA⊥面ABCD,AB∥CD,∠ABC=90°,AP=BC=2,AB=3,CD=1,E、F、M分别是BC、PA、PD的中点.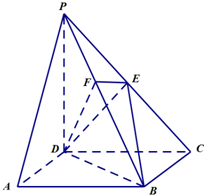 如图,在四棱锥P-ABCD中,侧面PDC⊥底面ABCD,已知△PDC是等腰直角三角形,其中∠PDC为直角,底面ABCD是边长为2的正方形,E是PC的中点,F是PB上的点.
如图,在四棱锥P-ABCD中,侧面PDC⊥底面ABCD,已知△PDC是等腰直角三角形,其中∠PDC为直角,底面ABCD是边长为2的正方形,E是PC的中点,F是PB上的点.