题目内容
某厂准备投资100万元用于A,B两个项目,据测算,投产后的年收益中,A项目是总投入的
,B项目则是总投入的算术根的两倍.
(1)若A项目的总投入用x(万元)表示,试确定两个项目的年总收益y(万元)的函数关系式;
(2)为使两个项目的年总收益达到最大,应怎样分配投入数?
| 1 |
| 5 |
(1)若A项目的总投入用x(万元)表示,试确定两个项目的年总收益y(万元)的函数关系式;
(2)为使两个项目的年总收益达到最大,应怎样分配投入数?
考点:根据实际问题选择函数类型
专题:函数的性质及应用
分析:(1)根据条件建立函数关系即可;
(2)根据函数结合二次函数的性质即可得到结论.
(2)根据函数结合二次函数的性质即可得到结论.
解答:
解:(1)依题意知A项目总投入为x万元时,B项目的总投入为100-x万元,
故两个项目的年总收益y=
x+2
,(0≤x≤100).
(2)令
=t,则x=100-t2,且t∈[0,10],
则函数等价为y=g(t)=20+2t-
t2=
(t-5)2+25,
∴当t=5时,函数取得最大值为25万元.
此时x=100-25=75万元,B项目的总投入为100-75=25万元,
故投入A项目为75万元,投入B项目为25万元时,两个项目的年总收益达到最大.
故两个项目的年总收益y=
| 1 |
| 5 |
| 100-x |
(2)令
| 100-x |
则函数等价为y=g(t)=20+2t-
| 1 |
| 5 |
| 1 |
| 5 |
∴当t=5时,函数取得最大值为25万元.
此时x=100-25=75万元,B项目的总投入为100-75=25万元,
故投入A项目为75万元,投入B项目为25万元时,两个项目的年总收益达到最大.
点评:本题主要考查函数的应用问题,利用二次函数的性质是解决本题的关键.

练习册系列答案
相关题目
在同一坐标系中,函数y=ax+a与y=ax的图象大致是( )
A、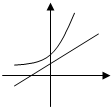 |
B、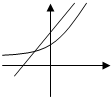 |
C、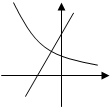 |
D、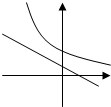 |
已知集合M={x|x2-2x≤0},N={x|
≤0},U=R,则图中阴影部分表示的集合是( )
| 3+x |
| 1-x |

| A、(-∞,0)∪(1,+∞) |
| B、(-∞,-3]∪(2,+∞) |
| C、(-∞,-3)∪(2,+∞) |
| D、(-∞,0]∪[2,+∞) |