题目内容

3．设全集U={1，3，5}，集合A={1，5}，则∁UA={3}．

分析 根据补集的定义写出运算结果即可．

解答 解：全集U={1，3，5}，集合A={1，5}，
则∁UA={3}．
故答案为：{3}．

点评 本题考查了集合的定义与应用问题，是基础题．

练习册系列答案
相关题目
13．通过$\widehat{{e}_{1}}$，$\widehat{{e}_{2}}$，…，$\widehat{{e}_{n}}$来判断模拟型拟合的效果，判断原始数据中是否存在可疑数据，这种分工称为（　　）
A．回归分析B．独立性检验分析C．残差分析D．散点图分析
14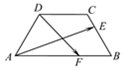．如图，等腰梯形ABCD中，AB=4，BC=CD=2，若E、F分别是边BC、AB上的点，且满足$\frac{BE}{BC}$=$\frac{AF}{AB}$=λ，当$\overrightarrow{AE}$•$\overrightarrow{DF}$=0时，则有（　　）
A．λ∈（$\frac{1}{8}$，$\frac{1}{4}$）B．λ∈（$\frac{1}{4}$，$\frac{3}{8}$）C．λ∈（$\frac{3}{8}$，$\frac{1}{2}$）D．λ∈（$\frac{1}{2}$，$\frac{5}{8}$）
11．将函数y=sin（x-$\frac{π}{12}$）图象上的点P（$\frac{π}{4}$，t）向左平移s（s＞0）个单位，得到点P′，若P′位于函数y=sin2x的图象上，则（　　）
A．t=$\frac{1}{2}$，s的最小值为$\frac{π}{6}$B．t=$\frac{\sqrt{3}}{2}$，s的最小值为$\frac{π}{6}$
C．t=$\frac{1}{2}$，s的最小值为$\frac{π}{12}$D．t=$\frac{\sqrt{3}}{2}$，s的最小值为$\frac{π}{12}$
18．已知y=f（x）是R上的奇函数，f（-1）=-1，且对任意x∈（-∞，0），f（x）=$\frac{1}{x}$f（$\frac{x}{x-1}$）都成立．
（1）求f（-$\frac{1}{2}$）、f（-$\frac{1}{3}$）的值；
（2）设an=f（$\frac{1}{n}$）（n∈N*），求数列{an}的递推公式和通项公式；
（3）记Tn=a1an+a2an-1+a3an-2+…+ana1，求$\underset{lim}{n→∞}$$\frac{{T}_{n+1}}{{T}_{n}}$的值．
8．已知函数f（x）满足f（x+1）=2x+3，若f（m）=3，则m=1．
15．下列说法中，正确的是④．（填序号）
①若函数f（x）满足f（x）＜f（x+1）对一切实数x成立，则f（x）是增函数；
②若函数满足|f（-x）|＜|f（x）|对一切实数x成立，则是奇函数或是偶函数；
③若函数f（x）满足f（1-x）=f（x+1）对一切实数x成立，则f（x）的图象关于y轴对称；
④若函数f（x）满足f（1-x）=f（x-1）对一切实数x成立，则f（x）的图象关于y轴对称．
12．已知集合A={x|x2-3x+2＜0}，B={x|3-x＞0}，则A∩B=（　　）
A．（2，3）B．（1，3）C．（1，2）D．（-∞，3）
13．2017是等差数列4，7，10，13，…的第几项（　　）
A．669B．670C．671D．672

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网