题目内容
若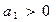 、
、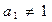 ,
,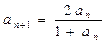
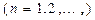
(1)求证: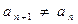 ;
;
(2)令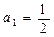 ,写出
,写出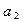 、
、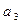 、
、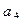 、
、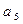 的值,观察并归纳出这个数列的通项公式
的值,观察并归纳出这个数列的通项公式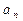 ;
;
(3)证明:存在不等于零的常数p,使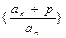 是等比数列,并求出公比q的值.
是等比数列,并求出公比q的值.
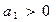 、
、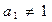 ,
,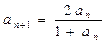
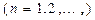
(1)求证:
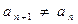 ;
;(2)令
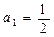 ,写出
,写出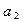 、
、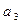 、
、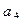 、
、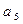 的值,观察并归纳出这个数列的通项公式
的值,观察并归纳出这个数列的通项公式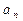 ;
;(3)证明:存在不等于零的常数p,使
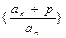 是等比数列,并求出公比q的值.
是等比数列,并求出公比q的值.(1)证明见解析
(2) 、
、 、
、 、
、 、
、 ,
, 
(3)证明见解析
(2)
 、
、 、
、 、
、 、
、 ,
, 
(3)证明见解析
(1)采用反证法. 若 ,即
,即 , 解得
, 解得 
从而 与题设
与题设 ,
, 相矛盾,
相矛盾,
故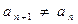 成立.
成立.
(2) 、
、 、
、 、
、 、
、 ,
,  .
.
(3)因为 又
又 ,
,
所以 ,
,
因为上式是关于变量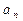 的恒等式,故可解得
的恒等式,故可解得 、
、 .
.
 ,即
,即 , 解得
, 解得 
从而
 与题设
与题设 ,
, 相矛盾,
相矛盾,故
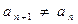 成立.
成立.(2)
 、
、 、
、 、
、 、
、 ,
,  .
.(3)因为
 又
又 ,
,所以
 ,
,因为上式是关于变量
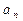 的恒等式,故可解得
的恒等式,故可解得 、
、 .
.
练习册系列答案
相关题目

 个棋子既不同行也不同列,则不同的放法有( )
个棋子既不同行也不同列,则不同的放法有( ) 种
种 种
种 种
种 种
种
 得其中
得其中 的值依次是____________.
的值依次是____________. ;(2)
;(2) .由以上两式成立,你能得到一个什么的推广?证明你的结论.
.由以上两式成立,你能得到一个什么的推广?证明你的结论. 且
且 ,求
,求 的值.(先观察
的值.(先观察 时的值,归纳猜测
时的值,归纳猜测 为非零向量,且
为非零向量,且 ,
, 不平行
不平行 (
( )的图像恒过点(0,
)的图像恒过点(0, )
) ”是 “
”是 “ ”的必要不充分条件
”的必要不充分条件 ”的否定是: “
”的否定是: “ ”
” ”是“
”是“ 在
在 上为增函数”的充要条件
上为增函数”的充要条件 的最小值是( )
的最小值是( )

