题目内容
2.设函数f(x)=log2(1+a•2x+4x),其中a为常数(1)当f(2)=f(1)+2,求a的值;
(2)当x∈[1,+∞)时,关于x的不等式f(x)≥x-1恒成立,试求a的取值范围.
分析 (1)直接计算出f(1)和f(2),根据条件解方程即可求得a;
(2)采用分离参数法,分离变量a,再根据函数的单调性求最值,得出a的取值范围.
解答 解:(1)∵f(x)=log2(1+a•2x+4x),
∴f(1)=log2(1+2a+4),f(2)=log2(1+4a+16),
由于f(2)=f(1)+2,
即log2(4a+17)=log2(2a+5)+2,
解得,a=-$\frac{3}{4}$;
(2)因为f(x)≥x-1恒成立,
所以,log2(1+a•2x+4x)≥x-1,
即,1+a•2x+4x≥2x-1,
分离参数a得,a≥$\frac{1}{2}$-(2x+2-x),
∵x≥1,∴(2x+2-x)min=$\frac{5}{2}$,此时x=1,
所以,a≥$\frac{1}{2}$-$\frac{5}{2}$=-2,
即实数a的取值范围为[-2,+∞).
点评 本题主要考查了对数函数的图象和性质,涉及对数的运算性质,以及不等式恒成立问题的解法,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.已知θ为锐角,sin2θ=-$\frac{7}{9}$,则sin($\frac{π}{4}$+θ)=( )
| A. | $±\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | -$\frac{1}{3}$ | D. | ±$\frac{\sqrt{2}}{3}$ |
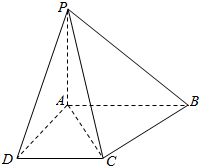 如图四棱锥P-ABCD中,PB=PC,底面ABCD是直角梯形,AB∥DC,∠ABC=60°,DC=1,AD=$\sqrt{3}$.
如图四棱锥P-ABCD中,PB=PC,底面ABCD是直角梯形,AB∥DC,∠ABC=60°,DC=1,AD=$\sqrt{3}$.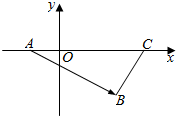 如图,在△ABC中,点A,C在x轴上,AB=4,∠BAC=30°,求向量$\overrightarrow{AB}$的坐标.
如图,在△ABC中,点A,C在x轴上,AB=4,∠BAC=30°,求向量$\overrightarrow{AB}$的坐标.