题目内容
已知sinα-cosα=-
,则sinα•cosα= .
| 4 |
| 5 |
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:把已知等式两边平方,利用完全平方公式及同角三角函数间基本关系化简,整理求出sinα•cosα的值即可.
解答:
解:把sinα-cosα=-
,两边平方得:(sinα-cosα)2=1-2sinαcosα=
,
则sinα•cosα=
,
故答案为:
| 4 |
| 5 |
| 16 |
| 25 |
则sinα•cosα=
| 9 |
| 50 |
故答案为:
| 9 |
| 50 |
点评:此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
由曲线y=f(x),直线x=a,x=b及x轴所围成的曲边梯形的面积是( )
A、
| ||
B、-
| ||
C、
| ||
D、|
|
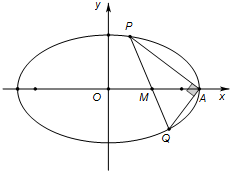 已知椭圆C:
已知椭圆C: 函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<2π)一个周期的图象如图所示,试确定A、ω、φ的值.
函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<2π)一个周期的图象如图所示,试确定A、ω、φ的值.