题目内容
如图,椭圆的中心在坐标原点,F为左焦点,A、B分别为长轴和短轴上的一个顶点,当FB⊥AB时,此类椭圆称为“优美椭圆”;类比“优美椭圆”,可推出“优美双曲线”的离心率为 .
【答案】分析:首先通过类比,得“优美双曲线”的虚轴一端与左焦点的连线,垂直于该点与右顶点连线.作出示意图,在RtABF中用射影定理,得b2=ac,结合双曲线a、b、c的关系和离心率的定义解一元二次方程,即可得到“优美双曲线”的离心率.
解答: 解:根据“优美椭圆”的定义,可得“优美双曲线”的虚轴一端与左焦点的连线,垂直于该点与右顶点连线.如图,设A是双曲线右顶点,B是虚轴上端点,F是左焦点
解:根据“优美椭圆”的定义,可得“优美双曲线”的虚轴一端与左焦点的连线,垂直于该点与右顶点连线.如图,设A是双曲线右顶点,B是虚轴上端点,F是左焦点
∵△ABF中,FB⊥AB,且AB⊥BF
∴OB2=OA×OF,即b2=ac
因此,c2-a2=ac,两边都除以a2并整理,得e2-e-1=0,解之得e= (舍负)
(舍负)
∴“优美双曲线”的离心率为
故答案为:
点评:本题通过“优美椭圆”类比到“优美双曲线”,求双曲线的离心率,着重考查了椭圆和双曲线基本概念和简单性质,考查了直角三角形中的相似三角形等知识,属于基础题.
解答:
 解:根据“优美椭圆”的定义,可得“优美双曲线”的虚轴一端与左焦点的连线,垂直于该点与右顶点连线.如图,设A是双曲线右顶点,B是虚轴上端点,F是左焦点
解:根据“优美椭圆”的定义,可得“优美双曲线”的虚轴一端与左焦点的连线,垂直于该点与右顶点连线.如图,设A是双曲线右顶点,B是虚轴上端点,F是左焦点∵△ABF中,FB⊥AB,且AB⊥BF
∴OB2=OA×OF,即b2=ac
因此,c2-a2=ac,两边都除以a2并整理,得e2-e-1=0,解之得e=
 (舍负)
(舍负)∴“优美双曲线”的离心率为

故答案为:

点评:本题通过“优美椭圆”类比到“优美双曲线”,求双曲线的离心率,着重考查了椭圆和双曲线基本概念和简单性质,考查了直角三角形中的相似三角形等知识,属于基础题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
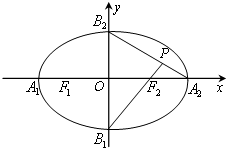 (2013•乌鲁木齐一模)如图,椭圆的中心在坐标原点O,顶点分别是A1,A2,B1,B2,焦点为F1,F2,延长B1F2与A2B2交于P点,若∠B1PA2为钝角,则此椭圆的离心率的取值范围为( )
(2013•乌鲁木齐一模)如图,椭圆的中心在坐标原点O,顶点分别是A1,A2,B1,B2,焦点为F1,F2,延长B1F2与A2B2交于P点,若∠B1PA2为钝角,则此椭圆的离心率的取值范围为( ) 如图,椭圆的中心在坐标原点O,左右焦点分别为F1,F2,右顶点为A,上顶点为B,离心率
如图,椭圆的中心在坐标原点O,左右焦点分别为F1,F2,右顶点为A,上顶点为B,离心率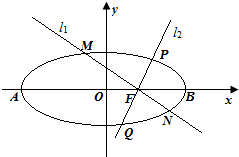 如图,椭圆的中心在坐标原点,长轴端点为A、B,右焦点为F,且
如图,椭圆的中心在坐标原点,长轴端点为A、B,右焦点为F,且 如图,椭圆的中心在坐标原点,F为左焦点,A、B分别为长轴和短轴上的一个顶点,当FB⊥AB时,此类椭圆称为“优美椭圆”;类比“优美椭圆”,可推出“优美双曲线”的离心率为
如图,椭圆的中心在坐标原点,F为左焦点,A、B分别为长轴和短轴上的一个顶点,当FB⊥AB时,此类椭圆称为“优美椭圆”;类比“优美椭圆”,可推出“优美双曲线”的离心率为 (2014•江门模拟)如图,椭圆Γ的中心在坐标原点O,过右焦点F(1,0)且垂直于椭圆对称轴的弦MN的长为3.
(2014•江门模拟)如图,椭圆Γ的中心在坐标原点O,过右焦点F(1,0)且垂直于椭圆对称轴的弦MN的长为3.