题目内容

如图，椭圆的中心在坐标原点O，左右焦点分别为F1，F2，右顶点为A，上顶点为B，离心率e=
35
，三角形△BF1F2的周长为16．直线y=kx（k＞0）与AB相交于点D，与椭圆相交于E，F两点．
（1）求该椭圆的标准方程．
（2）求四边形AEBF面积的最大值．
分析：（1）设中心在原点，长轴在x轴上的椭圆方程
x2
a2
+
y2
b2
=1(a＞b＞0)，焦距为2c．由题意可得a，c的关系，结合a2=b2+c2，可求a，b，c进而可求椭圆的方程；
（2）解法一：将直线的方程代入椭圆的方程，消去y得到关于x的一元二次方程：（16+25k2）x2=400
如图，设E（x1，kx1），F（x2，kx2），表示出四边形AEBF的面积，最后利用基本不等式求S的最大值；
解法二：由题设，|BO|=4，|AO|=5．再设y1=kx1，y2=kx2，表示出四边形AEBF的面积为S=S△BEF+S△AEF=4x2+5y2，最后利用基本不等式求其最大值即可．
解答：解：（1）设椭圆的方程为
x2
a2
+
y2
b2
=1(a＞b＞0)，焦距为2c，
依题意有
a2=b2+c2
e=
c
a
=
3
5
2a+2c=16
，解得
a=5
b=4
c=3

∴椭圆的方程为
x2
25
+
y2
16
=1，（5分）
（2）解法一：由
y=kx
x2
25
+
y2
16
=1
消去y，得（16+25k2）x2=400
如图，设E（x1，kx1），F（x2，kx2），其中x1＜x2，∴x1=-
20
16+25k2
，x2=
20
16+25k2
．①（8分）
∵直线AB的方程分别为
x
5
+
y
4
=1即4x+5y-20=0，
∴点E，F到AB的距离分别为h1=
|4x1+5kx1-20|
41
=
20(4+5k+
16+25k2
)
41
16+25k2
，h2=
|4x2+5kx2-20|
41
=
20(4+5k-
16+25k2
)
41
16+25k2
（10分）
又|AB|=
52+42
=
41
，
所以四边形AEBF的面积为
S=
1
2
|AB|(h1+h2)=
1
2
•
41
•
40(4+5k)
41
16+25k2
=
20(4+5k)
16+25k2
=20
16+25k2+40k
16+25k2

=20
1+
40k
16+25k2
≤20
1+
40k
2
16×25k2
=20
2
，
当且仅当16=25k2即k=
4
5
时，上式取等号．所以S的最大值为20
2
．（14分）
解法二：由题设，|BO|=4，|AO|=5．
设y1=kx1，y2=kx2，由①得x2＞0，y2=-y1＞0，且16
x
2
2
+25
y
2
2
=400
故四边形AEBF的面积为S=S△BEF+S△AEF=4x2+5y2（10分）=
(4x2+5y2)2
=
16
x
2
2
+25
y
2
2
+40x2y2
≤
2(16
x
2
2
+25
y
2
2
)
=20
2
，
当且仅当4x2=5y2时，上式取等号．所以S的最大值为20
2
．（14分）
点评：本题主要考查了由椭圆的性质求解椭圆方程，直线与椭圆的位置关系的应用，体现了方程的思想的应用，要注意弦长公式的应用．
练习册系列答案
相关题目
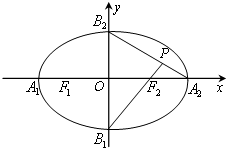（2013•乌鲁木齐一模）如图，椭圆的中心在坐标原点O，顶点分别是A1，A2，B1，B2，焦点为F1，F2，延长B1F2与A2B2交于P点，若∠B1PA2为钝角，则此椭圆的离心率的取值范围为（　　）
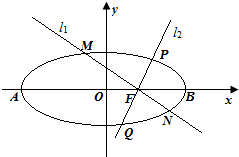如图，椭圆的中心在坐标原点，长轴端点为A、B，右焦点为F，且
AF
•
FB
=1，|
OF
|=1．
（Ⅰ）求椭圆的标准方程；
（Ⅱ）过椭圆的右焦点F作直线l1，l2，直线l1与椭圆分别交于点M、N，直线l2与椭圆分别交于点P、Q，且|
MP
|2+|
NQ
|2=|
NP
|2+|
MQ
|2，求四边形MPNQ的面积S的最小值．
如图，椭圆的中心在坐标原点，F为左焦点，A、B分别为长轴和短轴上的一个顶点，当FB⊥AB时，此类椭圆称为“优美椭圆”；类比“优美椭圆”，可推出“优美双曲线”的离心率为
1+
5
2
1+
5
2
．
（2014•江门模拟）如图，椭圆Γ的中心在坐标原点O，过右焦点F（1，0）且垂直于椭圆对称轴的弦MN的长为3．
（1）求椭圆Γ的方程；
（2）直线l经过点O交椭圆Γ于P、Q两点，NP=NQ，求直线l的方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网