Question

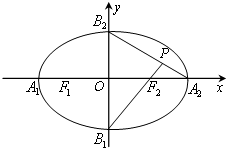（2013•乌鲁木齐一模）如图，椭圆的中心在坐标原点O，顶点分别是A₁，A₂，B₁，B₂，焦点为F₁，F₂，延长B₁F₂与A₂B₂交于P点，若∠B₁PA₂为钝角，则此椭圆的离心率的取值范围为（　　）

• A．(0，

  5 +1

  4

  )
• B．(

  5 +1

  4

  ，1)
• C．(0，

  5 -1

  2

  )
• D．(

  5 -1

  2

  ，1)

Answer 1

分析：由题意，∠B₁PA₂就是

B2A2

与

F2B1

的夹角，设椭圆的长半轴、短半轴、半焦距分别为a，b，c，则

B2A2

=（a，-b）、

F2B1

=（-c，-b），由向量的夹角为钝角可得-ac+b²＜0，把b²=a²-c²代入不等式，从而可求椭圆离心率的取值范围．

解答：解：由题意，∠B₁PA₂就是

B2A2

与

F2B1

的夹角，
设椭圆的长半轴、短半轴、半焦距分别为a，b，c，则

B2A2

=（a，-b）、

F2B1

=（-c，-b），
由向量的夹角为钝角知道

B2A2

与

F2B1

的数量积小于0，所以有：-ac+b²＜0，
把b²=a²-c²代入不等式得：a²-ac-c²＜0，除以a²得1-e-e²＜0，
即e²+e-1＞0，解得e＜

-1- 5

2

或e＞

-1+ 5

2

，
又0＜e＜1，所以

-1+ 5

2

＜e＜1，
所以椭圆离心率的取值范围为（

-1+ 5

2

，1）
故选D．

点评：本题考查椭圆的几何性质，解题的关键是利用道

B2A2

与

F2B1

的数量积小于0，建立不等式，属于中档题．