题目内容
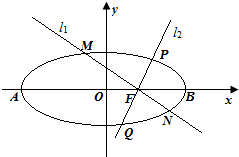 如图,椭圆的中心在坐标原点,长轴端点为A、B,右焦点为F,且
如图,椭圆的中心在坐标原点,长轴端点为A、B,右焦点为F,且| AF |
| FB |
| OF |
(Ⅰ)求椭圆的标准方程;
(Ⅱ)过椭圆的右焦点F作直线l1,l2,直线l1与椭圆分别交于点M、N,直线l2与椭圆分别交于点P、Q,且|
| MP |
| NQ |
| NP |
| MQ |
分析:(Ⅰ)设椭圆的方程,利用
•
=1,|
|=1,确定几何量,从而可得椭圆的方程;
(Ⅱ)利用|
|2+|
|2=|
|2+|
|2,确定l1⊥l2. 再分类讨论,分别计算四边形MPNQ的面积,利用基本不等式,可确定四边形形MPNQ的面积S的最小值.
| AF |
| FB |
| OF |
(Ⅱ)利用|
| MP |
| NQ |
| NP |
| MQ |
解答: 解:(Ⅰ)设椭圆的方程为
解:(Ⅰ)设椭圆的方程为
+
=1(a>b>0),
则由题意知c=1,
又∵
•
=1
∴(a+c)(a-c)=1=a2-c2
∴a2=2
∴b2=a2-c2=1,
故椭圆的方程为:
+y2=1;
(Ⅱ)设M(xM,yM),N(xN,yN),P(xP,yP),Q(xQ,yQ).
则由题意:|
|2+|
|2=|
|2+|
|2
整理得:(xN-xM)(xP-xQ)+(yN-yM)(yP-yQ)=0.
所以l1⊥l2.
①若直线l1,l2中有一条斜率不存在,不妨设l2的斜率不存在,则可得l2⊥x轴,
∴|MN|=2
,|PQ|=
,
故四边形MPNQ的面积S=
|PQ||MN|=
×2
×
=2.
②若直线l1,l2的斜率存在,设直线l1的方程:y=k(x-1)(k≠0),则
代入椭圆方程,消去y可得(2k2+1)x2-4k2x+2k2-2=0.
设M(x1,y1),N(x2,y2),则x1+x2=
,x1x2=
.
∴|MN|=
×
=
×
=
同理可求得,|PQ|=
.
故四边形MPNQ的面积:S=
|PQ||MN|=
×
×
=
≥
当且仅当k=±1时,取“=”.
综上,四边形形MPNQ的面积S的最小值为
.
 解:(Ⅰ)设椭圆的方程为
解:(Ⅰ)设椭圆的方程为| x2 |
| a2 |
| y2 |
| b2 |
则由题意知c=1,
又∵
| AF |
| FB |
∴(a+c)(a-c)=1=a2-c2
∴a2=2
∴b2=a2-c2=1,
故椭圆的方程为:
| x2 |
| 2 |
(Ⅱ)设M(xM,yM),N(xN,yN),P(xP,yP),Q(xQ,yQ).
则由题意:|
| MP |
| NQ |
| NP |
| MQ |
整理得:(xN-xM)(xP-xQ)+(yN-yM)(yP-yQ)=0.
所以l1⊥l2.
①若直线l1,l2中有一条斜率不存在,不妨设l2的斜率不存在,则可得l2⊥x轴,
∴|MN|=2
| 2 |
| 2 |
故四边形MPNQ的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
②若直线l1,l2的斜率存在,设直线l1的方程:y=k(x-1)(k≠0),则
代入椭圆方程,消去y可得(2k2+1)x2-4k2x+2k2-2=0.
设M(x1,y1),N(x2,y2),则x1+x2=
| 4k2 |
| 2k2+1 |
| 2k2-2 |
| 2k2+1 |
∴|MN|=
| 1+k2 |
| (x1+x2)2-4x1x2 |
| 1+k2 |
(
|
2
| ||
| 2k2+1 |
同理可求得,|PQ|=
2
| ||
| 2+k2 |
故四边形MPNQ的面积:S=
| 1 |
| 2 |
| 1 |
| 2 |
2
| ||
| 2k2+1 |
2
| ||
| 2+k2 |
| 4 | ||||
2+
|
| 16 |
| 9 |
当且仅当k=±1时,取“=”.
综上,四边形形MPNQ的面积S的最小值为
| 16 |
| 9 |
点评:本题考查椭圆的标准方程,考查向量知识的运用,考查基本不等式的运用,考查分类讨论的数学思想,正确表示四边形的面积是关键.

练习册系列答案
 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
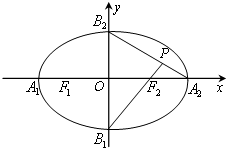 (2013•乌鲁木齐一模)如图,椭圆的中心在坐标原点O,顶点分别是A1,A2,B1,B2,焦点为F1,F2,延长B1F2与A2B2交于P点,若∠B1PA2为钝角,则此椭圆的离心率的取值范围为( )
(2013•乌鲁木齐一模)如图,椭圆的中心在坐标原点O,顶点分别是A1,A2,B1,B2,焦点为F1,F2,延长B1F2与A2B2交于P点,若∠B1PA2为钝角,则此椭圆的离心率的取值范围为( ) 如图,椭圆的中心在坐标原点O,左右焦点分别为F1,F2,右顶点为A,上顶点为B,离心率
如图,椭圆的中心在坐标原点O,左右焦点分别为F1,F2,右顶点为A,上顶点为B,离心率 如图,椭圆的中心在坐标原点,F为左焦点,A、B分别为长轴和短轴上的一个顶点,当FB⊥AB时,此类椭圆称为“优美椭圆”;类比“优美椭圆”,可推出“优美双曲线”的离心率为
如图,椭圆的中心在坐标原点,F为左焦点,A、B分别为长轴和短轴上的一个顶点,当FB⊥AB时,此类椭圆称为“优美椭圆”;类比“优美椭圆”,可推出“优美双曲线”的离心率为 (2014•江门模拟)如图,椭圆Γ的中心在坐标原点O,过右焦点F(1,0)且垂直于椭圆对称轴的弦MN的长为3.
(2014•江门模拟)如图,椭圆Γ的中心在坐标原点O,过右焦点F(1,0)且垂直于椭圆对称轴的弦MN的长为3.