题目内容
 在△ABC中,a,b,c分别是内角A,B,C的对边,AB=5, cos∠ABC=
在△ABC中,a,b,c分别是内角A,B,C的对边,AB=5, cos∠ABC=| 1 |
| 5 |
(Ⅰ) 若BC=4,求△ABC的面积S△ABC;
(Ⅱ) 若D是边AC中点,且BD=
| 7 |
| 2 |
考点:余弦定理
专题:解三角形
分析:(Ⅰ) 先求sin∠ABC,从而S△ABC=
|BA|•|BC|•sin∠ABC=4
;
(Ⅱ) 以BA,BC为邻边作如图所示的平行四边形ABCE,求出cos∠BCF,BE,CE,从而由余弦定理可得49=CB2+25-2×5×CB×(-
),可解CB的值.
| 1 |
| 2 |
| 6 |
(Ⅱ) 以BA,BC为邻边作如图所示的平行四边形ABCE,求出cos∠BCF,BE,CE,从而由余弦定理可得49=CB2+25-2×5×CB×(-
| 1 |
| 5 |
解答:
解:(Ⅰ) AB=5 , cos∠ABC=
,BC=4,
又∠ABC∈(0,π),所以sin∠ABC=
=
,
∴S△ABC=
|BA|•|BC|•sin∠ABC=
×5×4×
=4
.
(Ⅱ) 以BA,BC为邻边作如图所示的平行四边形ABCE,如图,
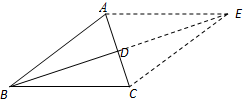
则cos∠BCE=-cos∠ABC=-
,BE=2BD=7,CE=AB=5,
在△BCE中,由余弦定理:BE2=CB2+CE2-2CB•CE•cos∠BCE.
即49=CB2+25-2×5×CB×(-
),
解得:CB=4.
| 1 |
| 5 |
又∠ABC∈(0,π),所以sin∠ABC=
| 1-cos2∠ABC |
2
| ||
| 5 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
2
| ||
| 5 |
| 6 |
(Ⅱ) 以BA,BC为邻边作如图所示的平行四边形ABCE,如图,

则cos∠BCE=-cos∠ABC=-
| 1 |
| 5 |
在△BCE中,由余弦定理:BE2=CB2+CE2-2CB•CE•cos∠BCE.
即49=CB2+25-2×5×CB×(-
| 1 |
| 5 |
解得:CB=4.
点评:本题主要考察了余弦定理的应用,考察数形结合与计算能力,属于中档题.

练习册系列答案
相关题目
“ab≠0”是“a2+b2≠0”的 ( )
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
如果f:a→b,称b是a的象,a是b的原象.给定映射f:(x,y)→(
,x2+y3),则点(6,-3)的象为( )
|
A、(
| ||||
B、(-
| ||||
C、(-
| ||||
| D、(6,-3)或(3,1) |
集合A={x|-2≤x≤a},B={y|y=2x+3,x∈A},C={y|y=x2,x∈A},且C⊆B,则实数a的取值范围是
( )
( )
A、
| ||
B、-
| ||
| C、2≤a≤3 | ||
| D、-1≤a≤3 |
在复平面内,复数
(i是复数单位)对应的点在第几象限( )
| 1 | ||
-
|
| A、一 | B、二 | C、三 | D、四 |