题目内容
一艘轮船在航行中的燃料费Q(元)和它的速度x(公里/小时)的立方成正比,已知在速度为每小时10公里时,燃料费是每小时6元,而其他与速度无关的费用是每小时96元.
(1)求此轮船在航行中的燃料费Q关于它的速度x的函数关系式;
(2)问轮船以多大速度航行时,能使行驶每公里的费用总和y最小?
(1)求此轮船在航行中的燃料费Q关于它的速度x的函数关系式;
(2)问轮船以多大速度航行时,能使行驶每公里的费用总和y最小?
考点:函数解析式的求解及常用方法,基本不等式
专题:应用题,导数的概念及应用
分析:(1)由轮船的速度为x,比例系数为k,(k>0),得出每小时的燃料费Q=kx3,求出k的值即可;
(2)求出费用总和y的解析式,对y求导,求出函数y取得极小值(即最小值)时x的值.
(2)求出费用总和y的解析式,对y求导,求出函数y取得极小值(即最小值)时x的值.
解答:
解::(1)∵轮船的速度为x,比例系数为k,(k>0),
∴每小时的燃料费为Q=kx3;
又∵x=10时,kx3=6,
解得k=
;
∴燃料费Q=
x3(x>0);
(2)轮船行驶每公里的费用总和为
y=(
x3+96)÷x=
x2+
;
对y求导,得y′=
x-
,
令y'=0,得v=20;
∴当0<x<20时,y'<0,函数y单调递减;
当x>20时,y'>0,函数y单调递增;
∴x=20时,函数y取得极小值,即为最小值.
∴轮船每小时行驶20公里时,驶每公里的费用总和最小.
∴每小时的燃料费为Q=kx3;
又∵x=10时,kx3=6,
解得k=
| 3 |
| 500 |
∴燃料费Q=
| 3 |
| 500 |
(2)轮船行驶每公里的费用总和为
y=(
| 3 |
| 500 |
| 3 |
| 500 |
| 96 |
| x |
对y求导,得y′=
| 6 |
| 500 |
| 96 |
| x2 |
令y'=0,得v=20;
∴当0<x<20时,y'<0,函数y单调递减;
当x>20时,y'>0,函数y单调递增;
∴x=20时,函数y取得极小值,即为最小值.
∴轮船每小时行驶20公里时,驶每公里的费用总和最小.
点评:本题考查了应用函数解决实际问题的例子,解题时应根据题意,建立函数的解析式,利用解析式求出问题的答案来,是中档题.

练习册系列答案
相关题目
集合A={x|lnx≥0},B={x|x2<16},则A∩B=( )
| A、(1,4) |
| B、[1,4) |
| C、[1,+∞) |
| D、[e,4) |
复数z的虚部为1,且
为纯虚数,其中i是虚数单位,则z=( )
| z |
| 1+i |
| A、-1-i | B、1+i |
| C、1-i | D、-1+i |
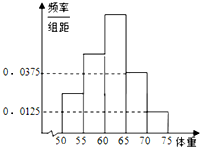 为了了解高三学生的身体状况,抽取了部分男生的体重,将所得的数据整理后,画出了频率分布直方图(如图).已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为15,则抽取的男生总人数是
为了了解高三学生的身体状况,抽取了部分男生的体重,将所得的数据整理后,画出了频率分布直方图(如图).已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为15,则抽取的男生总人数是