题目内容
已知椭圆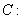
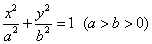 的左、右焦点分别为
的左、右焦点分别为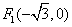 、
、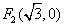 ,
,
椭圆上的点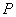 满足
满足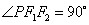 ,且
,且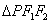 的面积
的面积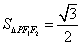 .
.
(Ⅰ)求椭圆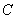 的方程;
的方程;
(Ⅱ)是否存在直线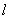 ,使
,使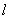 与椭圆
与椭圆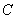 交于不同的两点
交于不同的两点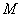 、
、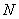 ,且线段
,且线段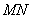 恰被直线
恰被直线
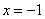 平分?若存在,求出
平分?若存在,求出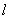 的斜率取值范围;若不存在,请说明理由.
的斜率取值范围;若不存在,请说明理由.
解:
(Ⅰ)由题意知: ,
,
 椭圆上的点
椭圆上的点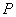 满足
满足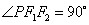 ,且
,且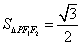 ,
,
 .
.
 ,
, .
.
 .
.
又 .
.  椭圆
椭圆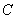 的方程为
的方程为 .
.
(Ⅱ)假设这样的直线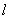 存在.
存在. 与直线
与直线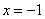 相交,
相交, 直线
直线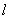 的斜率存在.
的斜率存在.
设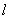 的方程为
的方程为 ,
,
由 得
得 .(*
.(*
 直线
直线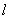 与椭圆
与椭圆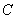 有两个交点,
有两个交点,
 (*)的判别式
(*)的判别式 ,即
,即 .①
.①
设 、
、 ,则
,则 .
.
 被直线
被直线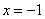 平分,可知
平分,可知 ,
,

 ,
, . ②
. ②
把②代入①,得 ,即
,即 .
.
 ,
, .
.
 或
或 .即存在满足题设条件的直线
.即存在满足题设条件的直线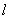 ,且
,且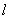 的斜率取值范围是
的斜率取值范围是
 .
.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 ,已知函数
,已知函数 ,若函数
,若函数 恰有两个零点,则
恰有两个零点,则 的取值范围为………( ).
的取值范围为………( ).
 .
. 
 .
. 
 .
. 
 .
.  是半圆
是半圆 的直径,
的直径, 在
在 与半圆相切于点
与半圆相切于点 ,
, ,若
,若 ,
, ,则
,则 .
. 
 是定义在
是定义在 上的函数,并满足
上的函数,并满足 当
当 时,
时, ,则
,则
 B.
B. C.
C. D.
D.
 满足:
满足: .
.  项和
项和 ;
; 的前
的前 ,且
,且 ,求
,求 满足
满足 ,则( )
,则( ) 有最大值4 B.
有最大值4 B. 有最小值
有最小值
 有最大值
有最大值 D.
D. 有最小值
有最小值
 的展开式中含有常数项,则最小的正整数
的展开式中含有常数项,则最小的正整数 等于 .
等于 . ,则
,则
 (B)
(B)  (C)
(C)  (D)
(D) 
