题目内容
求函数y=2sin( x+
x+ )的振幅、周期和初相,并作出它的图象.
)的振幅、周期和初相,并作出它的图象.
解:(1)函数y=2sin( x+
x+ )的振幅是2,周期是4π,初相是
)的振幅是2,周期是4π,初相是 ,
,
(2)列表:
画简图:
分析:(1)根据函数的解析式中A=2,ω= ,φ=
,φ= ,然后根据正弦型函数的性质,即可求出f(x)的周期、振幅、初相;
,然后根据正弦型函数的性质,即可求出f(x)的周期、振幅、初相;
(2)分别令 x+
x+ 取0,
取0, ,π,
,π, ,2π,并求出对应的(x,d(x))点,描点后即可得到函数在一个周期内的图象.
,2π,并求出对应的(x,d(x))点,描点后即可得到函数在一个周期内的图象.
点评:本题考查的知识点是五点法作函数y=Asin(ωx+φ)的图象,y=Asin(ωx+φ)中参数的物理意义,其中正弦型函数的图象的画法,性质是三角函数的重点内容之一,一定要熟练掌握.
 x+
x+ )的振幅是2,周期是4π,初相是
)的振幅是2,周期是4π,初相是 ,
,(2)列表:
| x |  |  |  |  | 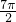 |
 x+ x+ | 0 |  | π |  | 2π |
y=2sin( x+ x+ ) ) | 0 | 2 | 0 | -2 | 0 |

分析:(1)根据函数的解析式中A=2,ω=
 ,φ=
,φ= ,然后根据正弦型函数的性质,即可求出f(x)的周期、振幅、初相;
,然后根据正弦型函数的性质,即可求出f(x)的周期、振幅、初相;(2)分别令
 x+
x+ 取0,
取0, ,π,
,π, ,2π,并求出对应的(x,d(x))点,描点后即可得到函数在一个周期内的图象.
,2π,并求出对应的(x,d(x))点,描点后即可得到函数在一个周期内的图象.点评:本题考查的知识点是五点法作函数y=Asin(ωx+φ)的图象,y=Asin(ωx+φ)中参数的物理意义,其中正弦型函数的图象的画法,性质是三角函数的重点内容之一,一定要熟练掌握.

练习册系列答案
相关题目
