题目内容

已知函数y=2sin(
x
2
+
π
3
)
（1）求函数y=2sin(
x
2
+
π
3
)的周期，最大值及取得最大值时相应的x的集合；
（2）指出函数y=2sin(
x
2
+
π
3
)的图象是由函数y=sinx（x∈R）的图象经过怎样的变化而得到的．
分析：（1）由公式T=
2π
ω
求周期即可，由正弦函数的性质，当相位是2kπ+
π
2
，k∈Z时函数取到最大值，故可令
x
2
+
π
3
=2kπ+
π
2
求函数取到最大值时相应的x的集合；
（2）由三角函数的图象变换规则对两个函数图象的关系进行研究即可得到变化方案．
解答：解：（1）由题，T=
2π
1
2
=4π（2分）
当2sin(
x
2
+
π
3
)=1，即
x
2
+
π
3
=2kπ+
π
2
，即x=4kπ+
π
3
，k∈Z时，y取得最大值2．（5分）
∴y取得最大值2时，x的取值集合为{x|x=4kπ+
π
3
，k∈Z}（6分）
（2）y=sinx
左移
π
3
个单位
，y=sin(x+
π
3
)
横坐标扩大到原来的2倍
，
y=sin(
x
2
+
π
3
 )
纵坐标扩大到原来的2倍
 y=2sin(
x
2
+
π
3
)（12分）
点评：本题考查三角周期性及求法，以及三角函数的最值求法，三角函数的图象变换规则，求解本题的关键是对函数的性质及相关的公式熟练掌握，本题有一易错点，即图象变换时作平移变换要注意自变量的系数是否为1，若否，则需要提取出系数再研究平移量是多少．
练习册系列答案
相关题目
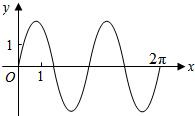精英家教网已知函数y=2sin（ωx+φ）（ω＞0））在区间[0，2π]的图象如图：那么ω=（　　）
A、1
B、2
C、
1
2
D、
1
3
已知函数y=2sin（wx+θ）为偶函数，其图象与直线y=2某两个交点的横坐标分别为x1，x2，若|x2-x1|的最小值为π，则该函数在区间（　　）上是增函数．
A、(-
π
2
，-
π
4
)
B、(-
π
4
，
π
4
)
C、(0，
π
2
)
D、(
π
4
，
3π
4
)
已知函数y=2sinωx（ω＞0）在[-
π
3
，
π
4
]上单调递增，则实数ω的取值范围为（　　）
已知函数y=
2
sin(2x+
π
4
)+2，求
（1）函数的最小正周期是多少？
（2）函数的单调增区间是什么？
（3）函数的图象可由函数y=
2
sin2x(x∈R)的图象如何变换而得到？
下列4个命题：
①已知函数y=2sin（x+?）（0＜?＜π）的图象如图所示，则φ=
π
6
或
5
6
π；
②在△ABC中，∠A＞∠B是sinA＞sinB的充要条件；
③定义域为R的奇函数f（x）满足f（1+x）=-f（x），则f（x）的图象关于点(
1
2
，0)对称；
④对于函数f（x）=x2+mx+n，若f（a）＞0，f（b）＞0，则f（x）在（a，b）内至多有一个零点；其中正确命题序号
②
②
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网