题目内容
3．若函数f（x）=$\frac{{2}^{x}-a}{{2}^{x}+1}$为奇函数，则实数a=（ ）| A． | 0 | B． | $\frac{1}{2}$ | C． | 1 | D． | 2 |
分析 根据奇函数f（x）满足f（0）=0这个结论，求得a的值．
解答 解：由函数f（x）=$\frac{{2}^{x}-a}{{2}^{x}+1}$为奇函数，可得f（0）=$\frac{1-a}{2}$=0，求得a=1，
故选：C．
点评 本题主要考查函数的奇偶性的性质，利用了奇函数f（x）满足f（0）=0这个结论，属于基础题．
练习册系列答案
名师伴你成长课时同步学练测系列答案
相关题目
11．已知向量$\overrightarrow a，\overrightarrow b$的夹角为60°，且|$\overrightarrow{a}$|=1，|$\overrightarrow{a}$-2$\overrightarrow{b}$|=$\sqrt{21}$，则|$\overrightarrow{b}$|=（ ）
| A． | $\sqrt{2}$ | B． | $\frac{3}{2}$ | C． | $\frac{5}{2}$ | D． | $2\sqrt{2}$ |
15．若$θ∈（\frac{π}{4}，\frac{π}{2}），sin2θ=\frac{1}{16}$，则cosθ-sinθ的值是（ ）
| A． | $\frac{{\sqrt{15}}}{4}$ | B． | $-\frac{{\sqrt{15}}}{4}$ | C． | $\frac{1}{4}$ | D． | $-\frac{1}{4}$ |
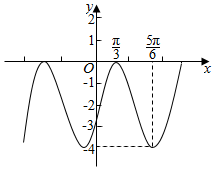已知函数f（x）=sinωx（sinωx+2$\sqrt{3}$cosωx）+sin（ωx-$\frac{π}{4}$）sin（ωx+$\frac{π}{4}$）（其中ω为常数，且ω＞0），函数g（x）=f（x）-$\frac{5}{2}$的部分图象如图所示．