题目内容
4．过圆x2+y2=4外一点M（4，-1）引圆的两条切线，则经过两切点的直线方程是（ ）| A． | 4x-y-4=0 | B． | 4x+y-4=0 | C． | 4x+y+4=0 | D． | 4x-y+4=0 |
分析 设切点是P（x1，y1）、Q（x2，y2），则以P为切点的切线方程是：x1x+y1y=4，以Q为切点的切线方程是：x2x+y2y=4，由此能求出过两切点P、Q的直线方程．
解答 解：设切点是P（x1，y1）、Q（x2，y2），
则以P为切点的切线方程是：x1x+y1y=4，
以Q为切点的切线方程是：x2x+y2y=4，
∵点M（4，-1）在两条切线上，则4x1-y1=4，4x2-y2=4
∴点P、Q的坐标满足方程：4x-y=4
∴过两切点P、Q的直线方程是：4x-y-4=0．
故选A．
点评 本题考查经过两个切点的直线方程的求法，是中档题，解题时要认真审题，注意圆的切线方程的性质的合理运用．
练习册系列答案
相关题目
15．抛物线y=4-x2与直线y=4x的两个交点为A、B，点P在抛物线上从A向B运动，当△PAB的面积为最大时，点P的坐标为（ ）
| A． | （-3，-5） | B． | （-2，0） | C． | （-1，3） | D． | （0，4） |
19．定义在（0，$\frac{π}{2}$），上的函数f（x），f′（x）是导函数，满足f（x）＜f′（x）tanx，则下列表达式正确的是（ ）
| A． | $\sqrt{3}$•f（$\frac{π}{4}$）＞$\sqrt{2}$•f（$\frac{π}{3}$） | B． | f（1）＞2•f（$\frac{π}{6}$）•sin1 | C． | $\sqrt{2}$•f（$\frac{π}{6}$）＞f（$\frac{π}{4}$） | D． | $\sqrt{3}$•f（$\frac{π}{6}$）＞f（$\frac{π}{3}$） |
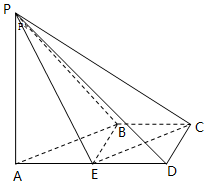如图，在四棱锥P-ABCD中，AD∥BC，∠ADC=∠PAB=90°，BC=CD=$\frac{1}{2}$AD=1，E为棱AD的中点，异面直线PA与CD所成的角为90°．
13．下列函数为奇函数的是（ ）
| A． | $y={x^{\frac{1}{2}}}$ | B． | y=x-1 | C． | y=x2 | D． | y=x3 |